Vấn đề 2. Chứng minh hai đường thẳng vuông góc
1. Phương pháp
Để chứng minh đường thẳng a vuông góc với đường thẳng b, ta có thể chứng minh:
• Đường thẳng a vuông góc với mặt phẳng (P) chứa b, hoặc
• Áp dụng định lí ba đường vuông góc.
2. Ví dụ 1
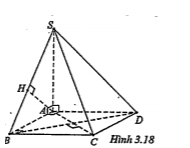
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA\[\bot \](ABCD).
a) Gọi AH là đường cao của tam giác SAB. Chứng minh rằng AH\[\bot \]BC
b) Chứng minh rằng SC vuông góc với BD.
| Lời giải a) Chứng minh AH\[\bot \]BC Ta có: BC\[\bot \]AB, BC\[\bot \]SA, \[\Rightarrow \]BC\[\bot \] (SAB) AH\[\subset \] (SAB) \[\Rightarrow \]BC\[\bot \]AH | Giải thích Ta chứng minh BC vuông góc với mặt phẳng (SAB). Chú ý rằng vì SA vuông góc với mặt phẳng (ABCD) nên SA vuông góc với mọi đường thẳng trong (ABCD)
|
| b) Chứng minh SC\[\bot \]BD Ta có: AC là hình chiếu của SC trên (ABCD) BD\[\bot \]AC (đường chéo hình vuông). Vậy BD\[\bot \]SC. | Áp dụng định lí ba đường vuông góc.
|
Ví dụ 2. Cho bốn điểm A, B, C, D bất kì
a) Chứng minh rằng \[\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0\]
b) Từ đó suy ra rằng trong một tứ diện nếu có hai cặp cạnh đối vuông góc thì cặp cạnh đối còn lại cũng vuông góc với nhau.
| Lời giải a) Chứng minh... \[\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}.(\overrightarrow{AD}-\overrightarrow{AC})\] \[=\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AC}\] (1) \[\overrightarrow{AC}.\overrightarrow{DB}=\overrightarrow{AC}.(\overrightarrow{AB}-\overrightarrow{AD})\] \[=\overrightarrow{AC}.\overrightarrow{AB}-\overrightarrow{AC}.\overrightarrow{AD}\] (2) \[\overrightarrow{AD}.\overrightarrow{BC}=\overrightarrow{AD}.(\overrightarrow{AC}-\overrightarrow{AB})\] \[=\overrightarrow{AD}.\overrightarrow{AC}-\overrightarrow{AD}.\overrightarrow{AB}\] (3) (1)+(2)+(3) ta có: \[\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0\]
| Giải thích Ta phân tích các vectơ \[\overrightarrow{CD},\overrightarrow{DB},\overrightarrow{BC}\] thành hiệu của các vectơ cùng gốc A. |
| b) Chứng minh tứ diện có... Giả sử tứ diện ABCD có: \[AB\bot CD,AC\bot BD\Rightarrow \overrightarrow{AB}.\overrightarrow{CD}=0,\overrightarrow{AC}.\overrightarrow{DB}\]=0 Khi đó:
\[\Rightarrow \overrightarrow{AD}.\overrightarrow{BC}=0\]\[\Rightarrow AD\bot BC\] | Thay \[\overrightarrow{AB}.\overrightarrow{CD}=0\], \[\overrightarrow{AC}.\overrightarrow{DB}=0\] vaò đẳng thức đã chứng minh ở câu a). |

.png)