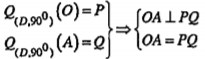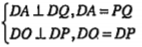C. CÂU HỎI VÀ BÀI TẬP
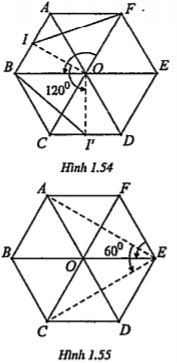
Bài 1.15. Cho lục giác đều ABCDEF, O là tâm đối xứng của nó; I là trung điểm của AB.
a) Tìm ảnh của tam giác AIF qua phép quay tâm O góc .png)
b) Tìm ảnh của tam giác AOF qua phép quay tâm E góc .png)
| Lời giải Ta có:
\[\Rightarrow {{Q}_{(O,{{120}^{0}})}}(\Delta AIF)=\Delta CI'B\] (H.1.54) Ta có:
\[\Rightarrow {{Q}_{(E,{{60}^{0}})}}(\Delta AOF)=\Delta CDO\] (H.1.55) |
|
Bài 1.16. Trong mặt phẳng Oxy cho các điểm A(3;3), B(0;5), C(1;1) và đường thẳng d: 5x-3y+15=0. Hãy xác định tọa độ các đỉnh của tam giác A'B'C’ và phương trình của đường thẳng d’ theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90°.
| Lời giải
| Giải thích
Đề nghị độc giả xem lại cách giải cụ thể trong ví dụ 2, vấn đề 1, bài 4.
|
| Ta có:
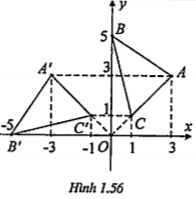
\[\Rightarrow {{Q}_{(O,{{90}^{0}})}}(\Delta ABC)=\Delta A'B'C'\] |
|
| Ta có:
Đường thẳng d' qua A’ và B’ nên có phương trình d': 3x+5y+15 =0.
| Đề nghị độc giả xem lại cách giải cụ thể trong ví dụ 3, vấn đề 1, bài 4.
|
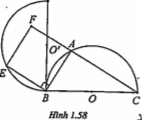
Bài 1.17. Cho nửa đường tròn tâm O đường kính BC. Điểm A chạy trên nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hình vuông ABEF. Chứng minh rằng E chạy trên một nửa đường tròn cố định.
| Lời giải Ta có:
nên khi A chạy trên nửa đường tròn tâm O đường kính BC thì E chạy trên nửa đường tròn tâm O' là ảnh của nửa đường tròn tâm O. | Giải thích Hướng dẫn: Tìm phép quay biến điểm A thành điểm E. Từ đó suy ra tập hợp của E
|
Bài 1.18. Cho tam giác ABC. Dựng về phía ngoài tam giác các hình vuông BCIJ, ACMN, ABEF và gọi O, P, Q lần lượt là tâm đối xứng của chúng.
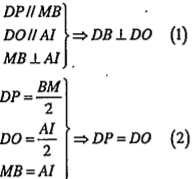
a) Gọi D là trung điểm của AB. Chứng minh rằng DOP là tam giác vuông cân đỉnh D.
b) Chứng minh AO vuông góc với PQ và AO = PQ.
| Lời giải a) Ta có:
Mặt khác:
(1) và (2) \[\Rightarrow \Delta DPO\]vuông cân đỉnh D | Giải thích Nhắc lại: Trong phép quay tâm I, góc quay \[\alpha \], ta có các kết quả sau: • Góc giữa hai đường thẳng bằng góc quay nếu góc quay là nhọn hoặc vuông. Trong trường hợp này góc quay bằng 90° nên góc giữa hai đường thẳng MB và AI là góc vuông, tức \[MB\bot AI\] • Bảo toàn khoảng cách giữa hai điểm nên MB = AI
|
| b) Ta có:
| Chú ý:
|

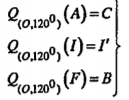
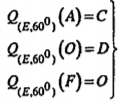
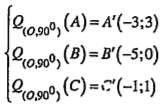
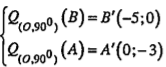
.png)
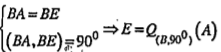
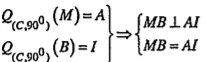
.png)