Chương II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG

§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG

A. CÁC KIẾN THỨC CẦN NHỚ

I. CÁC TÍNH CHẤT THỪA NHẬN

1. Tính chất thừa nhận 1: Tồn tại duy nhất một đường thẳng đi qua hai điểm phân biệt.

2. Tính chất thừa nhận 2: Tồn tại duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng.

• Mặt phẳng đi qua ba điểm không thẳng hàng A, B, C được ký hiệu là mp(ABC).

• Ngoài ba điểm A, B, C, mp(ABC) còn có vô số điểm khác nữa.

3. Tính chất thừa nhận 3: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

• Đường thẳng a nằm trong mặt phẳng \[(\alpha )\] được ký hiệu là: \[a\subset (\alpha )\]

• Hiển nhiên, ta có: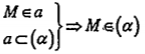

4. Tính chất thừa nhận 4: Nếu hai mặt phẳng có một điểm chung thì chúng còn có một điểm chung khác nữa.

5. Tính chất thừa nhận 5: Có ít nhất bốn điểm không đồng phẳng.

• Nếu có nhiều điểm cùng nằm trên một mặt phẳng thì ta nói chúng đồng phẳng

• Nếu không có mặt phẳng nào chứa các điểm đó thì ta nói chúng không đồng phẳng.

• Tiên đề 4 có thể phát biểu: “Có ít nhất bốn điểm không đồng phẳng”

6. Tính chất thừa nhận 6: Trên mỗi mặt phẳng, các kết qủa đã biết trong hình học phẳng đều đúng.

II. CÁC ĐỊNH LÝ

1: Định lý 1. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng chung này được gọi là giao tuyến của hai mặt phẳng.

a là giao tuyến của \[(\alpha )\] và \[\left( \beta \right)\]

2. Định lý 2. Tồn tại duy nhất một mặt phẳng đi qua một đường thẳng và một điểm nằm ngoài đường thẳng đó.

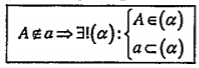
Ta ký hiệu mặt phẳng đi qua đường thẳng a và điểm C không thuộc a là: (C, a)

3. Định lý 3. Tồn tại duy nhất một mặt phẳng đi qua hai đường thẳng cắt nhau.

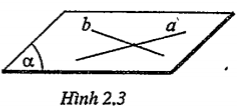
Ta ký hiệu mặt phẳng đi qua hai đường thẳng cắt nhau a và b là: (a, b).

4. HÌNH CHÓP

1. Định nghĩa. Trong mp\[(\alpha )\] cho đa giác và cho một điểm S nằm ngòai mp\[(\alpha )\]. Nối S với các đỉnh của đa giác ta được n-miền tam giác

Hình tạo bởi đa giác đã cho và n-miền tam giác đó gọi là hình chóp

Trong đó:

• S là đỉnh

• là mặt đáy

• là cạnh bên

• là cạnh đáy.

• Các miền tam giác là mặt bên của hình chóp.

Gọi tên

• Gọi tên hình chóp theo tên của đa giác đáy.

• Đặc biệt hình chóp tam giác được gọi là tứ diện. Trong tứ diện có thể lấy điểm nào làm đỉnh cũng được.

• Tứ diện đều là tứ diện có 4 mặt đều là tam giác đều. Suy ra, các cạnh của tứ diện đều thì bằng nhau.

2. Thiết diện của hình chóp và mặt phẳng

a) Định nghĩa. Mặt phẳng \[(\alpha )\]cắt các mặt (hoặc một số mặt) của hình chóp theo các đọan giao tuyến nối tiếp nhau tạo nên một đa giác phẳng được gọi là thiết diện của hình chóp và mặt phẳng đó.

b) Cách tìm thiết diện

Phương pháp chung để tìm thiết diện của một hình chóp với mặt phẳng \[(\alpha )\]là tìm các đọan giao tuyến của mp \[(\alpha )\] với các mặt của hình chóp. Thông thường, ta tìm “giao tuyến gốc” của mp\[(\alpha )\] với hình chóp. “Giao tuyến gốc” là một đọan giao tuyến của mp \[(\alpha )\]với một mặt nào đó của hình chóp mà ta đã thấy trước rồi. Từ đó ta tìm giao điểm của mp\[(\alpha )\] với các cạnh của hình chóp rồi suy ra thiết diện cần tìm.