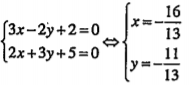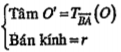Vấn đề 2. Dùng phép tịnh tiến để giải một số bài toán dựng hình

Vấn đề 2. Dùng phép tịnh tiến để giải một số bài toán dựng hình

1. Phương pháp

Để đựng một điểm M ta tìm cách xác định nó như là ảnh của một điểm đã biết qua một phép tịnh tiến, hoặc xem điểm M như là giao của một đường cố định với ảnh của một đường đã biết qua một phép tịnh tiến.

2. Ví dụ

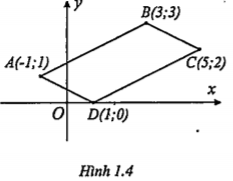
Ví dụ 1. Trong mặt phẳng tọa độ Oxy cho ba điểm A(-1;1), B(3;3), D(1;0). Tìm tọa độ đỉnh C sao cho tứ giác ABCD là hình bình hành.

Giải thích

Hướng dẫn. C là ảnh của D qua phép tịnh tiến theo vectơ \[\overrightarrow{AB}\]

Lời giải

Ta có \[\overrightarrow{AB}=(4;2)\], \[\overrightarrow{AD}=(2;-1)\]

\[\Rightarrow \]\[\overrightarrow{AB}\] và \[\overrightarrow{AD}\] không cùng phương

(vì \[\frac{4}{2}\ne \frac{2}{-1}\])

\[\Rightarrow \]Ba điểm A, B,D không thẳng hàng.

Khi đó:

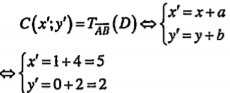
Vậy C(5;2)

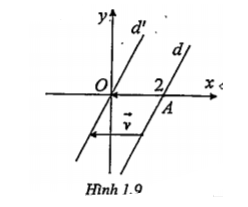
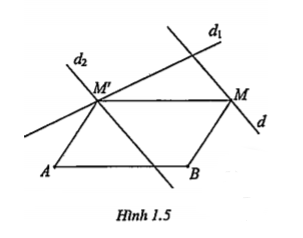
Ví dụ 2. Trong mặt phẳng cho hai đường thẳng cắt nhau d và d1, và hai điểm A, B không thuộc hai đường thẳng đó sao cho đường thẳng AB không song song hoặc trùng với d (hay d1). Hãy tìm điểm M trên d và điểm M’ trên d1 để tứ giác ABMM’ là hình bình hành.

Giải thích

Lời giải

Giả sử bài toán đã giải được. Ta có \[M\in d,M'\in {{d}_{1}}\], và tứ giác ABMM’ là hình bình hành. Vì ABMM’ là hình bình hành nên \[\overrightarrow{MM'}=\overrightarrow{BA}\], suy ra \[M'={{T}_{\overrightarrow{BA}}}(M).\] Gọi \[{{d}_{2}}={{T}_{\overrightarrow{BA}}}(d)\]thì \[M'\in {{d}_{1}}\cap {{d}_{2}}\].

Cách dựng.

• Dựng \[{{d}_{2}}={{T}_{\overrightarrow{BA}}}(d)\]

• Gọi giao điểm của d1 và d2, là M'

• Dựng \[M'={{T}_{\overrightarrow{BA}}}(M).\]

Khi đó tứ giác ABMM’ là hình bình hành.

Biện luận. Vì d và d1 cắt nhau và d2 // d nên d1 và d2 cắt nhau tại một điểm duy nhất. Vậy bài toán chỉ có một nghiệm hình duy nhất.

Bài 1.3.Trong mặt phẳng Oxy cho đường thẳng d:2x-y-4=0. Hãy tìm phép tịnh tiến vectơ có phương song song với trục Ox biến d thành đường thẳng d’ đi qua gốc tọa độ và viết phương trình của d’.

Bài 1.4. Trong mặt phẳng Oxy cho đường tròn có phương trình \[(C):{{x}^{2}}+{{y}^{2}}-4x+2y=0\] . Tìm ảnh (C') của (C) qua phép tịnh tiến theo vectơ \[\overrightarrow{v}=(2;-5)\].

Giải thích

Độc giả xem bài giải tương tự tại ví dụ 2.

Lời giải

Gọi M(x;y) \[\in \] (C), ta có:\[M'(x';y')={{T}_{\overrightarrow{v}}}(M)\]

Thay vào phương trình của (C), ta có:

\[{{\left( x'-2-2 \right)}^{2}}+{{\left( y'+5+1 \right)}^{2}}=9\]

\[{{\left( x'-4 \right)}^{2}}+{{\left( y'+6 \right)}^{2}}=9\]

Vậy phương trình của (C’) là:

\[{{\left( x-4 \right)}^{2}}+{{\left( y'+6 \right)}^{2}}=9\]

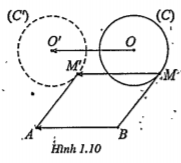
Bài 1.5. Cho đoạn thẳng AB và đường tròn (C) tâm O, bán kính r nằm về một phía của đường thẳng AB. Lấy điểm M trên (C) rồi dựng hình bình hành ABMM’. Tìm tập hợp các điểm M’ khi M di động trên (C).