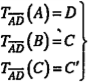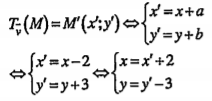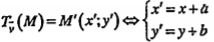B. DẠNG TOÁN CƠ BẢN
Vấn đề 1. Xác định ảnh của một hình qua phép tịnh tiến
1. Phương pháp
Để xác định ảnh của một hình qua phép tịnh tiến, ta dùng định nghĩa hoặc biểu thức của phép tịnh tiến.
2. Ví dụ
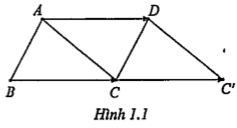
Ví dụ 1. Cho hình bình hành ABCD. Dựng ảnh của tam giác ABC qua phép tịnh tiến theo vectơ \[\overrightarrow{AD}\]
.png)
|
\[\Rightarrow {{T}_{\overrightarrow{AD}}}(\Delta ABC)=\Delta DCC'\] Chú ý. \[\overrightarrow{AD}=\overrightarrow{BC}\] |
|
Ví dụ 2. Trong mặt phẳng Oxy cho vectơ \[\overrightarrow{v}=(-2;3)\] và đường thẳng d có phương trình d: 3x-5y+3=0. Viết phương trình đường thẳng d’ là ảnh của đường thẳng d qua phép tịnh tiến \[{{T}_{\overrightarrow{v}}}\]
| Lời giải Cách 1. Dùng biểu thức của phép tịnh tiến Áp dụng biểu thức tọa độ của \[{{T}_{\overrightarrow{v}}}\] ta có:
Thay vào phương trình của d, ta có: 3(x'+2)-5(y'–3)+3=0 \[\Leftrightarrow \]3x' -5y' +24=0 Vậy phương trình của d’: 3x-5y+24=0
| Giải thích Các bước thực hiện: • Lấy điểm \[M(x,y)\in d\]. Gọi M’(x’;y’) là ảnh của M qua phép tịnh tiến \[{{T}_{\overrightarrow{v}}}\]. • Từ biểu thức tọa độ của phép tịnh tiến, tìm x, y theo x',y' và a,b. • Thay x, y vào phương trình của d. Từ đó suy ra phương trình của d’ |
| Cách 2. Đường thẳng đi qua một điểm và song song với một đường thẳng cho trước Lấy \[M\left( -1;0 \right)\in d\]. Khi đó
| Hướng dẫn • Lấy điểm \[M\in d\] (ta thường lấy M là giao điểm của d với trục Ox hoặc Oy). • Tìm ảnh M’ của M qua phép tịnh tiến đã cho. • Đường thẳng d’ qua M’ và song song với d. |
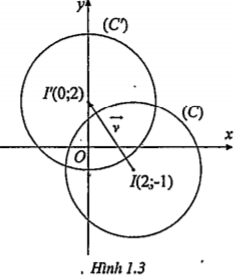
Gọi
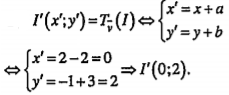
Do đó \[(C'):{{(x-0)}^{2}}+{{(y-2)}^{2}}=9\]
\[\Leftrightarrow (C'):{{x}^{2}}+{{y}^{2}}-4y+5=0\]
Vậy \[(C'):{{x}^{2}}+{{y}^{2}}-4y+5=0\]
Nhận xét. Để tìm phương trình của ảnh của một hình qua phép tịnh tiến theo vectơ \[\overrightarrow{v}\] ta nên làm theo cách 1.