C. CÂU HỎI VÀ BÀI TẬP
Bài 1.6. Trong mặt phẳng tọa độ Oxy, cho điểm M(3;-5), đường thẳng d có phương trình 3x+2y-6=0 và đường tròn \[(C):{{x}^{2}}+{{y}^{2}}-2x+4y-4=0\]. Tìm ảnh của M, d, (C) qua phép đối xứng trục Ox.
| M’ (x';y') =
\[\Rightarrow M(-3;5)\] |
|
| \[A\in d\cap Oy\Rightarrow A(0;3)\] \[B\in d\cap Ox\Rightarrow B(2;0)\]
.png) \[\Rightarrow \]d’: 3(x-0)-2(y+3)=0 \[\Leftrightarrow \] d’: 3x-2y-6=0 | .png)
|
|
Vậy \[(C'):{{(x-1)}^{2}}+{{(y-2)}^{2}}=9\] |
|
Bài 1.7. Trong mặt phẳng Oxy cho đường thẳng d có phương trình x-5y+z=0 và đường thẳng d’ có phương trình 5x - y - 13 = 0. Tìm phép đối xứng qua trục biến d thành d’.
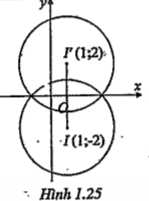
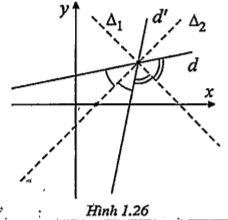
| Vì d và d’ cắt nhau nên trục đối xứng A cần tìm là đường phân giác của góc tạo bởi d và d'. Từ đó suy ra \[\Delta \] có phương trình: \[\frac{\left| x-5y+7 \right|}{\sqrt{{{1}^{2}}+{{(-5)}^{2}}}}=\frac{\left| 5x-y-13 \right|}{\sqrt{{{5}^{2}}+{{(-1)}^{2}}}}\] Vậy có hai trục đối xứng biến d thành d’ là \[{{\Delta }_{1}}\] : x+y-5=0 và \[{{\Delta }_{2}}\]: x-y-1=0
| Để viết phương trình đường phân giác của góc tạo bởi hai đường thẳng cắt nhau, ta áp dụng tính chất: Mọi điểm nằm trên đường phân giác của góc thì cách đều hai cạnh của góc đó. Áp dụng công thức tính khoảng cách từ điểm \[d(M,d)=\frac{\left| Ax+By+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\] \[d(M,d')=\frac{\left| A'x+B'y+C' \right|}{\sqrt{A{{'}^{2}}+B{{'}^{2}}}}\] \[M\in \Delta \Leftrightarrow d(M,d)=d(M,d')\] \[\frac{\left| Ax+By+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}=\frac{\left| A'x+B'y+C' \right|}{\sqrt{A{{'}^{2}}+B{{'}^{2}}}}\] Đây chính là phương trình đường phân giác của góc tạo bởi hai đường thẳng cắt nhau d và d’.
|
Bài 1.8. Tìm các trục đối xứng của hình vuông.
| Lời giải Hình vuông có 4 trục đối xứng gồm hai đường trung trực của các cạnh và hai đường thẳng đi qua hai đường chéo của hình vuông đó (cách giải tương tự ví dụ của vấn đề 2).
| Giải thích
|
Bài 1.9. Cho hai đường thẳng c, d cắt nhau và hai điểm A, B không thuộc hai đường thẳng đó. Hãy dựng điểm C trên c, điểm D trên d sao cho tứ giác ABCD là hình thang cân nhận AB làm một cạnh đáy (không cần biện luận).
| Lời giải • Phân tích: Giả sử bài toàn đã dựng xong. Ta có:
• Cách dựng: Dựng trung trực n của AB. Dựng Dựng Khi đó ABCD là hình thang cân cần dựng • Chứng minh: Theo cách dựng thì tứ giác
nên nó là hình thang cân.
| Giải thích Cần chú ý rằng hình thang cân có một trục đối xứng là đường trung trực của cạnh đáy.
|
Bài 1.10. Cho đường thẳng d và hai điểm A, B không thuộc d nhưng nằm cùng phía đối với d. Tìm trên d điểm M sao cho tổng các khoảng cách từ đó đến A và B là bé nhất.
| Lời giải Gọi Khi đó với mỗi điểm M\[\in \]d, ta có: MA + MB=MA' + MB nên MA + MB bé nhất \[\Leftrightarrow \]MA' + MB bé nhất \[\Leftrightarrow \] M, A, B thẳng hàng \[\Leftrightarrow M\in A'B\cap d\]
| Giải thích
|

.png)
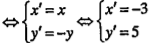
.png)
.png)
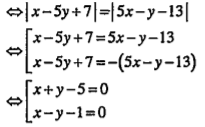
.png) đến đường thẳng d: Ax+By+C=0 và đường thẳng d’: A’x+B’y+C’=0 là:
đến đường thẳng d: Ax+By+C=0 và đường thẳng d’: A’x+B’y+C’=0 là:.png)

.png) . Gọi \[C\in d'\cap c\]
. Gọi \[C\in d'\cap c\] .png)
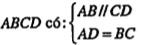
.png) \[\Rightarrow \] MA = MA’
\[\Rightarrow \] MA = MA’