§3. PHÉP ĐỐI XỨNG TRỤC

A. CÁC KIẾN THỨC CẦN NHỚ

I. ĐỊNH NGHĨA

• Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.

Phép đối xứng trục d thường được kí hiệu là Đđ. Như vậy:

M’=Đđ(M)\[\Leftrightarrow \overrightarrow{{{M}_{0}}M'}=-\overrightarrow{{{M}_{0}}M}\]

với là hình chiếu vuông góc của M trên d.

• Đường thẳng d được gọi là trục đối xứng của hình ℋ nếu Đđ biến ℋ thành chính nó. Khi đó ℋ được gọi là hình có trục đối xứng.

II. BIỂU THỨC TỌA ĐỘ

Trong mặt phẳng tọa độ Oxy, với mỗi điểm M(x;y), gọi M'(x;y)=Đđ(M)

• Nếu chọn d là trục Ox thì:

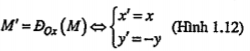
• Nếu chọn d là trục Oy thì:

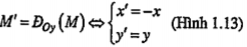
III. TÍNH CHẤT

Phép đối xứng trục:

1) Bảo toàn khoảng cách giữa hai điểm bất kì (H. 1.14):

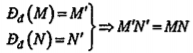
2) Biến một đường thẳng thành một đường thẳng (H. 1.15): Đđ(d)=d’

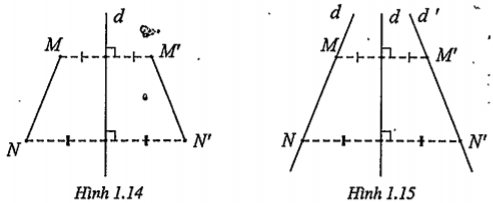
3) Biến một đoạn thẳng thành đoạn thẳng bằng đoạn thẳng đã cho:

Đđ(MN)= M’N’\[\Rightarrow \] M'N' = MN

4) Biến một tam giác thành tam giác bằng tam giác đã cho (H. 1.16)

Đđ\[(\Delta MNP)=\Delta M'N'P'\Rightarrow \Delta MNP=\Delta M'N'P'\]

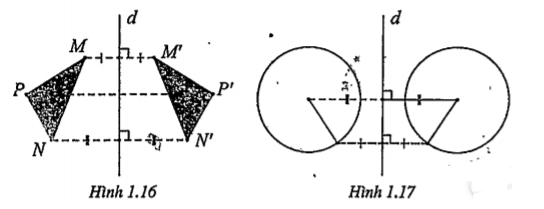
5) Biến một đường tròn thành đường tròn có cùng bán kính (H. 1.17)

Đđ(I,R)=(I’;R)