B. DẠNG TOÁN CƠ BẢN
Vấn đề 1. Chứng minh hai mặt phẳng vuông góc
1. Phương pháp
Để chứng minh hai mặt phẳng vuông góc, ta có thể dùng một trong hai cách sau:
Cách 1. Áp dụng định lý:
Hai mặt phẳng vuông góc với nhau khi và chỉ khi một trong chúng chứa đường thẳng vuông góc với đường thẳng còn lại.
\[\left( P \right)\supset a,a\bot \left( Q \right)\Leftrightarrow \left( Q \right)\bot \left( P \right)\]
Như vậy, việc chứng minh hai mặt phẳng vuông góc quy về việc chứng minh một đường thẳng vuông góc với một mặt phẳng.
Cách 2. Chứng minh góc giữa hai mặt phẳng bằng 90°.
2. Ví dụ
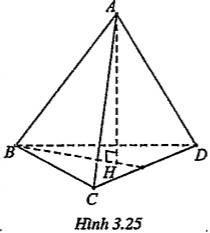
Ví dụ. Cho tứ diện ABCD có AH vuông góc với mp(BCD) tại H và AB\[\bot \]CD. Chứng minh rằng (ABH)\[\bot \] (ACD).
| Lời giải Ta có: AH\[\bot \] (BCD) (BCD) \[\supset \]CD => AH\[\bot \]CD Như vậy: CD\[\bot \]AH CD\[\bot \]HB => CD\[\bot \] (ABH) Mặt khác: (ACD) => (ACD)\[\bot \] (ABH). | Giải thích Ta chứng minh CD vuông góc với mặt phẳng (ABH).
|

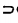 CD
CD