B. DẠNG TOÁN CƠ BẢN
Vấn đề 1. Chứng minh mặt phẳng song song với mặt phẳng
1. Phương pháp
Để chứng minh hai mặt phẳng song song, ta dùng định lí 9:
Nếu mp\[\left( \alpha \right)\] chứa hai đường thẳng a, b cắt nhau và hai đường thẳng này cùng song song với một mp\[\left( \beta \right)\] cho trước thì hai mp\[\left( \alpha \right)\] và \[\left( \beta \right)\] song song với nhau.
2. Ví dụ
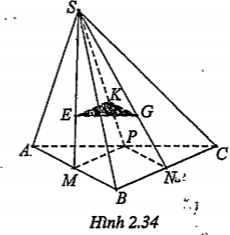
Ví dụ. Cho tứ diện SABC. E G, K lần lượt là trọng tâm của các tam giác SAB, SBC, SCA.
a) Chứng minh GK//(SAB), EK//(SBC), EG// (SCA).
b) Chứng minh (EGK)//(ABC).
| Lời giải Chứng minh GK//(SAB), EK//(SBC), EG// (SCA). Gọi M, N, P lần lượt là trung điểm của AB, BC và CA thì E G, K thuộc AM, SN, SP. \[\Delta SPN\Rightarrow \frac{SK}{SP}=\frac{SG}{SN}=\frac{2}{3}\] \[\Rightarrow KG//PN\] (1) Mặt khác: PN là đường trung bình của \[\Delta \]ABC nên: PN // AB (2) (1)và (2)\[\Rightarrow KG//AB\] (3)
| Giải thích Áp dụng định lí 4 để chứng minh đường thẳng song song với mặt phẳng.
|
| Như vậy: KG//AB, AB\[\subset \] (SAB) \[\Rightarrow \]KG//(SAB) Tương tự, ta có: EK//(SBC), EG//(SAC). |
|
| b) Chứng minh (EGK)//(ABC) Tương tự, ta có: EK//MP Như vậy: KG// PN EK // PM KG,EK cắt nhau trong (EGK) PN, PM\[\subset \] (ABC) \[\Rightarrow \] (EGK)//(ABC) | Ta chứng minh trong mặt phẳng (EGK) có hai đường thẳng cắt nhau và song song với hai đường thẳng trong mặt phẳng (ABC).
|