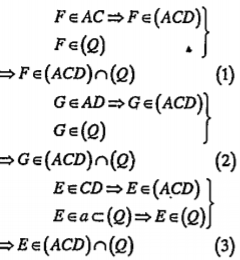Vấn đề 3. Chứng minh ba điểm thẳng hàng
1. Phương pháp
Để chứng minh ba điểm (trở lên) thẳng hàng ta có thể chứng minh ba điểm ấy cùng thuộc hai mặt phẳng phân biệt nào đó. Lúc này, ba điểm ấy nằm trên giao tuyến của hai mặt phẳng nên chúng thẳng hàng.
2. Ví dụ:
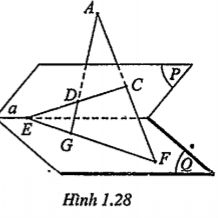
Ví dụ. Gọi a là giao tuyến của hai mặt mặt phẳng (P) và (Q), A là điểm không nằm trên cả hai mặt phẳng này; C và D là hai điểm nằm trên mp(P). Gọi E là giao điểm của a với CD; F và G lần lượt là giao điểm của AC, AD với mp(Q). Chứng minh rằng ba điểm E, F và G thẳng hàng.
| Lời giải Vì D và C thuộc mp(P), A không thuộc (P) nên A, C và D không thẳng hàng. Do đó, tồn tại mặt phẳng (ACD). Ta có:
Như vậy, ba điểm F, G, E nằm trên giao tuyến của hai mặt phẳng (ACD) và (Q) nên chúng thẳng hàng. | Giải thích Hướng dẫn: Ta chứng minh ba điểm E, F, G nằm trên giao tuyến của hai mặt phẳng (Q) và (ACD).
|