Vấn đề 2. Tìm phép đồng dạng biến hình ℋ thành hình ℋ’

1. Phương pháp

Tìm cách biểu thị phép đồng dạng đó như là kết quả của việc thực hiện liên tiếp các phép đồng dạng quen biết.

2. Ví dụ

Ví dụ 1. Cho hai hình vuông có cạnh a và b. Chứng minh rằng luôn có một phép đồng dạng biến hình này thành hình kia.

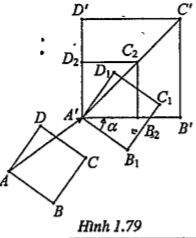
Lời giải

Giả sử có hai hình vuông ABCD cạnh a và A'B'C'D' cạnh b (H. 1.79).

• Phép tịnh tiến \[{{T}_{\overrightarrow{AA'}}}\] biến hình vuông ABCD thành hình vuông

• Phép quay với biến hình vuông thành hình vuông

Giải thích

Các bước thực hiện:

•Bước 1: Tìm ảnh của hình vuông ABCD qua phép \[{{T}_{\overrightarrow{AA'}}}\]

• Bước 2: Tìm ảnh của hình vuông qua phép \[{{Q}_{(A,a)}}\]

• Phép vị tự với \[k=\frac{A'D'}{AD}\] biến hình vuông thành hình vuông A'B'C'D'.

Vậy phép đồng dạng có được bằng cách thực hiện liên tiếp các phép biến hình \[{{T}_{\overrightarrow{AA'}}}\], và sẽ biến hình vuông ABCD thành hình vuông A’B’C’D’.

• Bước 3: Phép vị tự với \[k=\frac{A'D'}{AD}\] biến hình vuông thành hình vuông A'B'C'D'.

Chú ý. Trong phép vị tự ta cần chú ý rằng tỉ số vị tự là \[k=\frac{A'D'}{A'{{D}_{2}}}\] nhưng vì =AD nên ta có \[k=\frac{A'D'}{AD}\]