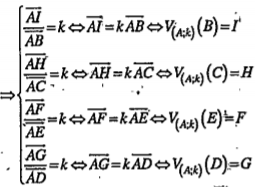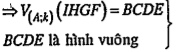Vấn đề 3. Dùng phép vị tự để dựng hình
1. Phương pháp
Ta thực hiện các bước sau:
• Bước 1: Xác định phép vị tự biến hình H phải dựng thành hình H’.
• Bước 2: Dựng hình H’ rồi suy ra hình H.
2. Ví dụ
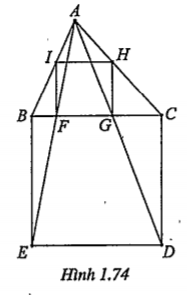
Ví dụ 1. Dựng hình vuông nội tiếp tam giác cho trước. (Hình vuông nội tiếp tam giác là hình vuông có hai đỉnh liên tiếp nằm trên một cạnh, hai đỉnh còn lại nằm trên hai cạnh kia của tam giác).
| Lời giải • Phân tích: Giả sử đã đựng được hình vuông IHGF nội tiếp tam giác ABC cho trước: F, G nằm trên cạnh BC, I và H lần lượt thuộc hại cạnh còn lại. Thực hiện phép vị tự tâm A, tỉ số \[k=\frac{IH}{BC}\] thì hình vuông IHGF sẽ biến thành hình vuông BCDE. • Cách dựng: Dựng hình vuông BCDE sao cho BCDE và tam giác ABC không cùng phía đối với đường thẳng BC. Gọi \[F\in AE\cap BC,G\in AD\cap BC\] Qua F, G dựng hai đường thẳng song song với CD cắt AB, AC lần lượt tại I, H. Khi đó hình vuông IHGF là hình vuông cần dựng. • Chứng minh: Theo cách dựng thì tứ giác IHGF nội tiếp tam giác ABC. Áp dụng định lí Ta – let, ta có: \[\frac{\overrightarrow{AI}}{\overrightarrow{AB}}=\frac{\overrightarrow{AH}}{\overrightarrow{AC}}=\frac{\overrightarrow{AF}}{\overrightarrow{AE}}=\frac{\overrightarrow{AG}}{\overrightarrow{AD}}=k\]
| Giải thích
|
|
\[\Rightarrow \]IHGF cũng là hình vuông. • Biện luận: Ta luôn chỉ có một hình vuông duy nhất BCDE nằm khác phía của tam giác ABC đối với đường thẳng AB nên chỉ có duy nhất một điểm F và một điểm G. Vậy bài toán luôn có một nghiệm hình duy nhất. |
|