B. DẠNG TOÁN CƠ BẢN

Vấn đề 1. Chứng minh đường thẳng vuông góc với mặt phẳng

1. Phương pháp

Để chứng minh đường thẳng a vuông góc với mặt phẳng (P), ta có thể chứng minh:

• Đường thẳng a vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (P), hoặc

• Đường thẳng a//b mà b\[\bot \] (P).

2. Ví dụ

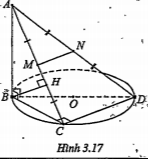
Ví dụ. Trong mặt phẳng (P) cho đường tròn tâm O, đường kính BD. Trên đường thẳng vuông góc với mặt phẳng (P) tại B lấy điểm A. Trên đường tròn (O) lấy điểm C.

a) Gọi M, N lần lượt là trung điểm của AC và AD. Chứng minh rằng MN vuông góc với mặt phẳng (ABC).

b) Chứng minh rằng tứ diện ABCD có các mặt đều là tam giác vuông.

Lời giải

a) Chứng minh MN\[\bot \] (ABC)

Ta có: AB\[\bot \](P), (P)\[\supset \] CD\[\Rightarrow \]AB\[\bot \]CD

Mặt khác:CD\[\bot \]BC

\[\Rightarrow \]CD\[\bot \] (ABC)

mà MN // CD

CD\[\bot \] (ABC)\[\Rightarrow \] MN\[\bot \] (ABC)

Giải thích

Chú ý rằng khi AB vuông góc với (P) thì AB vuông góc với mọi đường thẳng trong (P).

b) Chứng minh các mặt của tứ diện...

Ta có: vuông tại C

(BCD nội tiếp nửa (O))

AB\[\bot \](P), (P)\[\supset \] BC\[\Rightarrow \] AB\[\bot \]BC

\[\Rightarrow \]\[\Delta \]ABC vuông tại B.

Tương tự, \[\Delta \]ABD vuông tại B.

Mặt khác:CD\[\bot \] (ABC)\[\Rightarrow \] \[\Delta \]ACD vuông tại C.