CÂU HỎI VÀ BÀI TẬP ÔN TẬP CHƯƠNG I
Bài 1.31. Trong mặt phẳng Oxy cho đường thẳng d: 3x-5y+3=0 và vectơ \[\overrightarrow{v}\]=(2;3). Hãy viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến theo vectơ \[\overrightarrow{v}\].
| Đáp số: d': 3x-5y +12=0 | Đề nghị độc giả xem lại cách giải tương tự tại ví dụ 2, vấn đề 1, bài 1. |
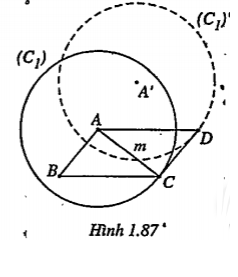
Bài 1.32. Cho hình bình hành ABCD có AB cố định, đường chéo AC = m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm C thuộc một đường tròn xác định.
| Lời giải Vì CA = m không đổi nên tập hợp của C là đường tròn (C1) tâm A bán kính m. Mặt khác \[D={{T}_{\overrightarrow{AB}}}(C)\] nên khi C chạy trên (C1) thì D chạy trên (C1)’ là ảnh của (C1) qua phép tịnh tiến theo vectơ \[\overrightarrow{AB}\]. (C1)’ có tâm A’ là ảnh của A qua phép tịnh tiến nói trên, bán kính bằng m. | Giải thích • Để tìm tập hợp của D, ta hãy tìm tập hợp của C là đường tròn (cần chú ý rằng C cách A một khoảng không đổi m). • Vì AB cố định nên ta thấy D là ảnh của C qua phép tịnh tiến theo vectơ \[\overrightarrow{AB}\].
|
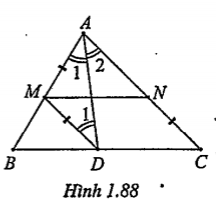
Bài 1.33. Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.
| Lời giải • Phân tích: Giả sử bài toán đã giải xong, ta có \[M\in AB,N\in AC\] và Vẽ MD// CN (D\[\in \]BC). Tứ giác MDCN là hình bình hành nên: MD = NC. Mặt khác: AM = NC Do đó MD = AM\[\Rightarrow \Delta MAD\] cân tại M.
\[\Rightarrow \] AD là phân giác trong của góc\[\widehat{BAC}\]. Từ đó suy ra cách dựng như sau: • Cách dựng: Dựng phân giác trong AD của \[\widehat{BAC}\]. Kẻ DM//AC, M\[\in \]AB. Dựng N là ảnh của M qua phép tịnh tiện theo vectơ \[\overrightarrow{DC}\]. M, N là hai điểm cần dựng. • Chứng minh: Ta có
\[N={{T}_{\overrightarrow{DC}}}(M)\Rightarrow \overrightarrow{MN}=\overrightarrow{DC}\] \[\Rightarrow MN=CN\] (2) (1) và (2) \[\Rightarrow AM=NC\] | Giải thích
• \[\widehat{{{A}_{1}}}=\widehat{{{A}_{2}}}\] (AD là phân giác \[\widehat{BAC}\]
• \[\widehat{{{D}_{1}}}=\widehat{{{A}_{2}}}\] (DM//AC) • \[\overrightarrow{MN}=\overrightarrow{DC}\] \[\Rightarrow \] MNCD là hình bình hành \[\Rightarrow MD=CN\] |
Bài 1.34. Trong mặt phẳng Oxy cho đường thẳng d: 3x - 2y - 6=0.
a) Viết phương trình của đường thẳng d1 là ảnh của d qua phép đối xứng trục Oy.
b) Viết phương trình của đường thẳng d2 là ảnh của d qua phép đối xứng qua đường thẳng \[\Delta \]:x+y-2=0
| Đáp số: a) d1:3x+2y+6=0 b) d2: 2x-3y-4=0. | Đề nghị độc giả xem cách giải tương tự tại ví dụ 3, vấn đề 1, bài 3 |
Bài 1.35. Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Một điểm M chạy trên đường tròn (trừ hai điểm A, B). Hãy xác định hình bình hành AMBN. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.
| Lời giải Gọi I là tâm của hình bình hành AMBN, khi đó N là ảnh của M qua phép đối xứng tâm I. Vì vậy, khi M chạy trên (C) thì N chạy trên (C’) là ảnh của (C) qua phép đối xứng tâm I nói trên.
| Giải thích Chú ý. Đường tròn (C) có tâm O’ là ảnh của O qua phép đối xứng tâm I, bán kính bằng bán kính của (C)
|
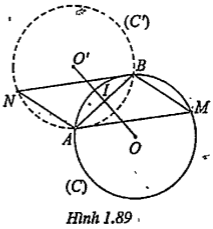
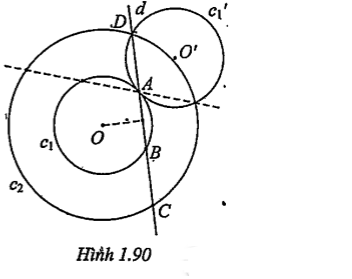
Bài 1.36. Cho hai đường tròn có cùng tâm O, bán kính lần lượt R, r (R> r). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D sao cho CD = 3AB.
| Lời giải. • Phân tích: Ta có: \[CD=3AB\Leftrightarrow AD=AB=BC\]
nên có thể xem D là ảnh của B qua phép đối xứng tâm A. Gọi c’1 là ảnh của c1 qua phép đối xứng tâm A thì • Cách dựng: Dựng đường tròn c’1 là ảnh của c1 qua phép đối xứng tâm A. Dựng D là giao điểm của c1’ và c2. Dựng đường thẳng d qua A, D cắt c1 và c2 lần lượt tại B, C. d là đường thẳng cần dựng. • Chứng minh: Theo cách dựng thì d cắt c1, c2 lần lượt tại A,B,C,D.
\[\Rightarrow CD=3AB\] • Biện luận: Số nghiệm của bài toán phụ thuộc vào số giao điểm của c1’ và c2 nên bài toán có thể có 0, 1, 2 nghiệm hình . | Giải thích Gọi I là trung điểm của AB thì
Ta có: \[CD=3AB\] \[\Leftrightarrow AD+AB+BC=3AB\] \[\Leftrightarrow AD+BC=2AB\] \[\Leftrightarrow AD=BC=AB\]
|
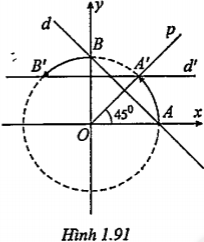
Bài 1.37. Trong mặt phẳng Oxy cho đường thẳng d: x+y-2=0. Hãy viết phương trình của đường thẳng d' là ảnh của d qua phép quay tâm O góc .png) .
.
| Gợi ý giải Gọi \[A(2;0)\in d\cap Ox\] \[B(0;2)\in d\cap Oy\] thì \[A'(\sqrt{2};\sqrt{2})={{Q}_{(O;{{45}^{0}})}}(A)\] \[B'(-\sqrt{2};\sqrt{2})={{Q}_{(O;{{45}^{0}})}}(B)\] d’ đi qua A’, B’ nên d’: \[y=\sqrt{2}\]
| Đề nghị đọc giả xem lại cách giải tương tự tại bài 1.27
|
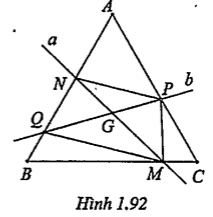
Bài 138. Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P, AB tại Q, đồng thời góc giữa a, b bằng 60°. Chứng minh rằng tứ giác MPNQ là hình thang cân.
| Lời giải Ta có:
| Giải thích • Vì G là tâm của tam giác ABC nên GA=GB=GC Do đó khi thực hiện phép quay \[{{Q}_{\left( G,{{120}^{0}} \right)}}\] thì \[A\mapsto B\mapsto C\mapsto A\] |
|
\[\Rightarrow \] MPNQ là hình thang cân. |
|
Bài 139. Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng: \[\overrightarrow{A'B'}.\overrightarrow{A'C'}={{k}^{2}}.\overrightarrow{AB}.\overrightarrow{AC}\].
| Lời giải Gọi F là phép đồng dạng biến \[A\mapsto A',B\mapsto B',C\mapsto C'\] Theo định nghĩa phép đồng dạng, ta có: \[B'C'=kBC\Rightarrow B'C{{'}^{2}}={{k}^{2}}B{{C}^{2}}\] \[\Rightarrow \overrightarrow{B'C{{'}^{2}}}={{k}^{2}}\overrightarrow{B{{C}^{2}}}\] \[\Rightarrow {{\left( \overrightarrow{A'C'}-\overrightarrow{A'B'} \right)}^{2}}={{k}^{2}}{{\left( \overrightarrow{AC}-\overrightarrow{AB} \right)}^{2}}\] \[\Rightarrow A'C{{'}^{2}}+A'B{{'}^{2}}-2\overrightarrow{A'C'}.\overrightarrow{A'B'}={{k}^{2}}\left( A{{C}^{2}}+A{{B}^{2}}-2\overrightarrow{AC}.\overrightarrow{AB} \right)\] \[\Rightarrow \overrightarrow{A'C'}.\overrightarrow{A'B'}={{k}^{2}}\overrightarrow{AC}.\overrightarrow{AB}\] (đpcm) | Giải thích Để ý rằng, trong phép đồng dạng tỉ số k, ta có: \[A'C'=kAC,A'B'=kAB\] nên \[A'C{{'}^{2}}={{k}^{2}}A{{C}^{2}},A'B{{'}^{2}}={{k}^{2}}A{{B}^{2}}\] |
Bài 1.40. Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng. Chứng minh rằng nếu \[\overrightarrow{AB}=p\overrightarrow{AC}\] thì \[\overrightarrow{A'B'}=p\overrightarrow{A'C'}\] trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A, C thì điểm B’ nằm giữa hai điểm A’ và C’.
| Lời giải. Gọi F là phép đồng dạng biến \[A\mapsto {A}',B\mapsto {B}',C\mapsto {C}'\] Ta có: \[\overrightarrow{AB}=p\overrightarrow{AC}\Rightarrow \overrightarrow{\frac{AB}{\overrightarrow{AC}}}=p\] Mặt khác, định nghĩa phép đồng dạng cho:
\[\overrightarrow{A'B'}=p\overrightarrow{A'C'}\] Giả sử A, B, C thẳng hàng và B ở giữa A và C khi đó: \[\overrightarrow{AB}=k\overrightarrow{AC}\] với Suy ra \[\overrightarrow{A'B'}=k\overrightarrow{A'C}\] với (2) chứng tỏ A’,B’,C’ thẳng hàng và B’ ở giữa A’ và C’.
| Giải thích Từ (1) suy ra (2), ta có thể chứng minh như sau: Định nghĩa phép đồng dạng cho ta: \[\overrightarrow{A'B'}=k\overrightarrow{AB}\Rightarrow \overrightarrow{\frac{A'B'}{\overrightarrow{AB}}}=k\] (3) \[\overrightarrow{A'C'}=k\overrightarrow{AC}\] (4) Thay (3) vào (4): \[\overrightarrow{A'C'}=\overrightarrow{\frac{A'B'}{\overrightarrow{AB}}}.\overrightarrow{AC}\] (5) Giả thiết \[\overrightarrow{AB}=k\overrightarrow{AC}\] (6) Thay (6) vào (5): \[\overrightarrow{A'C'}=\overrightarrow{\frac{A'B'}{k\overrightarrow{AC}}}\overrightarrow{AC}\] \[\overrightarrow{A'B'}=k\overrightarrow{A'C'}\] (đpcm) |
Bài 1.41. Trong mặt phẳng Oxy xét phép biến hình F biến mỗi điểm M(x; y) thành M’(2x– 1;-2y + 3). Chứng minh rằng F là một phép đồng dạng.
| Lời giải Lấy điểm N(x’;y’). Khi đó: F(N)=N'(2x' –1;-2y'+3) Ta có: \[M'N{{'}^{2}}={{(2x'-1-2x+1)}^{2}}+{{\left( -2y'+3+2y-3 \right)}^{2}}\] \[\Leftrightarrow M'N{{'}^{2}}=4\left[ {{\left( x'-x \right)}^{2}}+{{\left( y'-y \right)}^{2}} \right]\] Mặt khác: \[M{{N}^{2}}={{\left( x'-x \right)}^{2}}+{{\left( y'-y \right)}^{2}}\] Do đó \[M'N{{'}^{2}}=4M{{N}^{2}}\Leftrightarrow M'N'=2MN\] Chứng tỏ F là một phép đồng dạng với tỉ số k =2 | Hướng dẫn • Lấy điểm N bất kì. Tìm ảnh N’ của N qua phép biến hình F • Hãy chứng tỏ M'N' =k.MN. Kết luận F là một phép đồng dạng. Chú ý. Nhắc lại công thức khoảng cách giữa hai điểm A,B: \[AB=\sqrt{{{\left( {{x}_{B}}-{{x}_{A}} \right)}^{2}}+{{\left( {{y}_{B}}-{{y}_{A}} \right)}^{2}}}\] |
Bài 1.42. Dựng tam giác ABC vuông cân tại A có C là một điểm cho trước, còn hai điểm A, B lần lượt thuộc hai đường thẳng a, b song song với nhau cho trước.
| Lời giải • Phân tích: Giả sử bài toán đã giải được. Ta thấy B là ảnh của A qua phép đồng dạng F có được bằng cách thực hiện liên tiếp phép quay \[{{Q}_{(C;\pm {{45}^{0}})}}\] và phép vị tự \[{{V}_{(C;\sqrt{2})}}\] nên B là giao điểm của đường thẳng a’ (ảnh của a) với b. Từ đó suy ra cách dựng. • Cách dựng Dựng a’ là ảnh của a qua phép đồng đạng F. Dựng điểm\[B\in b\cap a'\]. Dựng trung trực d của BC cắt a tại A. Tam giác ABC là tam giác cần dựng. • Chứng minh: Theo cách dựng thì tam giác ABC cân tại A và \[\widehat{B}=\widehat{C}={{45}^{0}}\] nên \[\widehat{A}={{90}^{0}}\]do đó nó vuông cân tại A. Ngoài ra, ta còn có A\[\in \]a, B\[\in \]b. • Biện luận: Bài toán luôn có hai nghiệm hình. | Giải thích Vì tam giác ABC vuông cân tại A nên \[BC=AC\sqrt{2}\]. Chú ý rằng phép quay \[{{Q}_{(C;\pm {{45}^{0}})}}\] biến điểm A thành điểm A’; phép vị tự \[{{V}_{(C;\sqrt{2})}}\] biến A’ thành B.
|

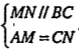
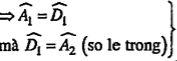
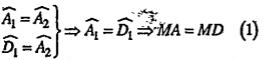
.png) . Từ đó suy ra cách dựng như sau:
. Từ đó suy ra cách dựng như sau: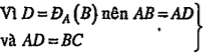
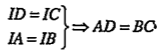
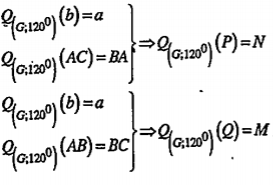
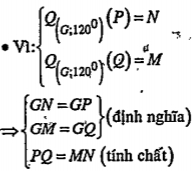

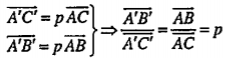
.png) (1)
(1).png) (2)
(2).png)