B. DẠNG TOÁN CƠ BẢN
Vấn đề 1. Xác định giao tuyến của hai mặt phẳng (dùng quan hệ song song)
1. Phương pháp
Áp dụng hệ qủa của định lý 2. Tức là ta chỉ cần tìm một điểm chung của hai mặt phẳng và phương của giao tuyến ấy.
2. Ví dụ
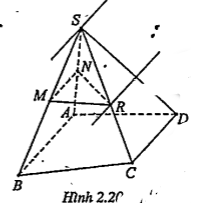
Ví dụ. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). M, N lần lượt là trung điểm của SB và SA, R là một điểm bất kỳ trên SC, nhưng không trùng với S.
a) Chứng minh MN // CD.
b) Xác định giao tuyến của hai mặt phẳng (SCD) và (MNR).
c) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
| Lời giải a) Chứng minh MN // CD MN là đường trung bình của \[\Delta \]SAB nên: MN // AB (1) AB // CD (đáy của hình thang) (2) (1) và (2) suy ra: MN // CD. | Hướng dẫn Áp dụng định lí 3. |
| b. Giao tuyến của (SCD) và (MNR) Ta có: MN\[\subset \] (SAB), CD\[\subset \] (SCD) MN // CD R\[\in \] (MNR)\[\cap \] (SCD) ⇒ (MNR)\[\cap \] (SCD)=RQ//MN (Q\[\in \]SD)
| Áp dụng hệ quả của định lí 2.
|
| c) Giao tuyến của (SAB) và (SCD) Ta có: AB\[\subset \](SAB), CD\[\subset \] (SCD) AB//CD S\[\in \] (SAB)\[\cap \] (SCD) \[\Rightarrow \] (SAB)\[\cap \] (SCD)=Sx//AB//CD | Áp dụng hệ quả của định lí 2. |