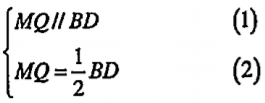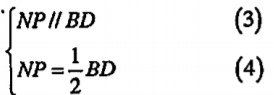Vấn đề 2. Chứng minh hai đường thẳng song song
1. Phương pháp
Để chứng minh hai đường thẳng a và b song song với nhau, ta có thể chứng minh:
• Nếu đã biết a và b đồng phẳng rồi thì ta sử dụng các phương pháp chứng minh trong hình học phẳng như: Cạnh đối của hình bình hành, định lý Thales đảo, đường trung bình của tam giác,...
• Nếu chưa thấy a và b đồng phẳng thì có thể dùng định lý 2, hệ qủa của nó hoặc định lý 3.
2. Ví dụ
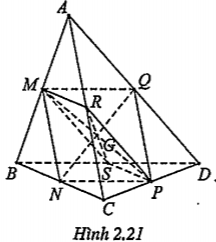
Ví dụ. Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của AB, BC, CD, DA, AC và BD. Chứng minh rằng các đoạn thẳng MP, NQ và RS đồng quy tại trung điểm G của mỗi đọan. (Người ta gọi điểm G là trọng tâm của tứ diện ABCD đã cho).
| Chứng minh MNPQ là hình bình hành • MQ là đường trung bình của \[\Delta \]ABD nên:
• NP là đường trung bình của \[\Delta \]CBD nên:
(1) và (2)\[\Rightarrow \] MQ//NP (5) (2) và (4)\[\Rightarrow \]MQ=NP (6) (5) và (6)\[\Rightarrow \] MNPQ là hình bình hành | Hướng dẫn • Ta chứng minh MNPQ và MRPS là hình bình hành. • Để ý rằng hai hình bình hành này có chung đường chéo MP. |
| Suy ra hai đường chéo NQ và MP cắt nhau tại trung điểm G của mỗi đường (*) Chứng minh MRPS là hình bình hành Tương tự, ta có MRPS là hình bình hành. Suy ra hai đường chéo RS và MP cắt nhau tại trung điểm G của mỗi đường (**) (*) và (**) suy ra các đoạn thẳng MP, NQ và RS đồng quy tại trung điểm G của mỗi đọan. |
|