Bài 2. HAI ĐƯỜNG THẲNG VUÔNG GÓC
A. CÁC KIẾN THỨC CẦN NHỚ
I. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ TRONG KHÔNG GIAN
1. Góc giữa hai vectơ
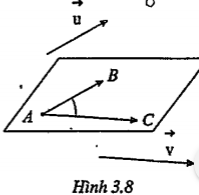
Cho \[\overrightarrow{u}\] và \[\overrightarrow{v}\] là hai vectơ bất kì trong không gian. Từ một điểm A bất kì vẽ \[\overrightarrow{AB}=\overrightarrow{u}\], \[\overrightarrow{AC}=\overrightarrow{v}\]. Khi đó ta gọi góc \[\widehat{BAC}\left( {{0}^{0}}\le \widehat{BAC}\le {{180}^{0}} \right)\] là góc giữa hai vectơ \[\overrightarrow{u}\] và \[\overrightarrow{v}\], kí hiệu \[(\overrightarrow{u},\overrightarrow{v})\]
Ta có: \[(\overrightarrow{u},\overrightarrow{v})=\widehat{BAC}\]
2. Tích vô hướng
Tích vô hướng của hai vectơ \[\overrightarrow{u}\] và \[\overrightarrow{v}\] (khác 0) trong không gian là một số thực được kí hiệu là \[\overrightarrow{u}.\overrightarrow{v}\] và được xác định bởi công thức:
\[\overrightarrow{u}.\overrightarrow{v}=\left| \overrightarrow{u} \right|.\left| \overrightarrow{v} \right|.\cos \left( \overrightarrow{u}.\overrightarrow{v} \right)\]
Nếu \[\overrightarrow{u}=0\] hoặc \[\overrightarrow{v}=0\] thì ta quy ước\[\overrightarrow{u}.\overrightarrow{v}=0\].
3. Tính chất.
Với ba vectơ \[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\]bất kì trong không gian và mọi số thực k, ta có:
\[\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}\]
\[\overrightarrow{a}.(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}\overrightarrow{.c}\]
\[k\overrightarrow{a}.\overrightarrow{b}=k.(\overrightarrow{a}.\overrightarrow{b})+\overrightarrow{a}.k\overrightarrow{.b}\]
\[{{\overrightarrow{a}}^{2}}\ge 0;{{\overrightarrow{a}}^{2}}=0\Leftrightarrow \overrightarrow{a}=0\]
4. Vectơ chỉ phương của đường thẳng
a) Vectơ \[\overrightarrow{u}\ne \overrightarrow{0}\] được gọi là vectơ chỉ phương của đường thẳng d nếu giá của nó song song hoặc trùng với d.
b) Nếu \[\overrightarrow{u}\ne \overrightarrow{0}\] là vectơ chỉ phương của d thì vectơ \[k\overrightarrow{u}\] với \[k\ne \overrightarrow{0}\] cũng là vectơ chỉ phương của d.
c) Một đường thẳng trong không gian hoàn toàn được xác định nếu biết trước một điểm và một vectơ chỉ phương của nó
5. Một số ứng dụng của tích vô hướng
a) Tính độ dài đoạn thẳng AB:
\[AB=\left| \overrightarrow{AB} \right|=\sqrt{\overrightarrow{A{{B}^{2}}}}\]
b) Xác định góc giữa hai vectơ:
\[\cos (\overrightarrow{a},\overrightarrow{b})=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a}.\overrightarrow{b} \right|}\]
II. GÓC GIỮA HAI ĐƯỜNG THẲNG
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm bất kì lần lượt song song với a và b
III. HAI ĐƯỜNG THẲNG VUÔNG GÓC
1. Định lý 20. Hai đường thẳng a và b được gọi là vuông góc nếu góc giữa chúng bằng 90°. Kí hiệu a\[\bot \]b
2. Định lý 21. Nếu \[\overrightarrow{u}\] và \[\overrightarrow{v}\] là hai vectơ chỉ phương của a và b thì:
\[\overrightarrow{a}\bot \overrightarrow{b}\Leftrightarrow \overrightarrow{u}.\overrightarrow{v}=0\]
3. Định lý 22. Nếu a//b và c vuông góc với một trong hai đường thẳng đó thì c vuông góc với đường thẳng còn lại.
