Bài 5. PHÉP QUAY
A. CÁC KIẾN THỨC CẦN NHỚ
I. ĐỊNH NGHĨA
Cho điểm O và góc lượng giác \[\alpha \] .Phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho góc lượng giác (OM';OM)=\[\alpha \] được gọi là phép quay tâm O góc \[\alpha \]. Kí hiệu: Q(O,\[\alpha \])
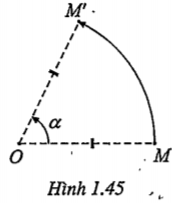
Như vậy:
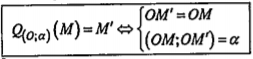
Nhận xét.
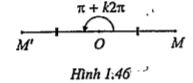
• Phép quay tâm O góc quay \[\alpha \]=\[\pi \]+k2\[\pi \] (k\[\in \]Z) là phép đối xứng tâm O. (H.146)
• Phép quay tâm O góc quay \[\alpha \]=k2\[\pi \] (k\[\in \]Z) là phép đồng nhất.
II. TÍNH CHẤT
Phép quay:
• Bảo toàn khoảng cách giữa hai điểm bất kì (H. 1.47)
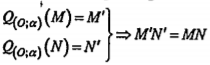
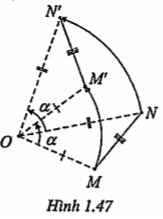
• Biến một đường thẳng thành một đường thẳng
• Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho
• Biến một tam giác thành tam giác bằng tam giác đã cho
• Biến một đường tròn thành một đường tròn có cùng bán kính.
Chú ý. Giả sử phép quay tâm I góc \[\alpha \] biến đường thẳng d thành đường thẳng d’
Khi đó:
• Nếu \[0<\alpha \le \frac{\pi }{2}\]thì góc giữa d và d’ bằng \[\alpha \].
• Nếu \[\frac{\pi }{2}<\alpha <\pi \] thì góc giữa d và d’ bằng \[\pi -\alpha \].