Vấn đề 2. Xác định giao điểm của đường thẳng và mặt phẳng

1. Phương pháp

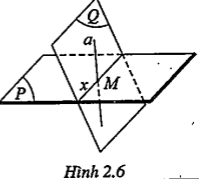
Để tìm giao điểm của đường thẳng d với mp(P), ta làm như sau:

• Chọn mặt phẳng phụ (Q) chứa đường thẳng a.

• Tìm giao tuyến x của (P) và (Q)

• Trong (Q), gọi M là giao điểm của a và x

• Như vậy, M là điểm chung của a và (P).

Trong thực hành, ta có thể trình bày như sau:

\[\Rightarrow M\in a\cap (P)\]

2. Ví dụ

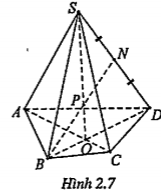
Ví dụ. Cho tứ giác ABCD (không có cặp cạnh đối nào song song) nằm trong mặt phẳng \[\left( \alpha \right)\]. S là điểm không nằm trên \[\left( \alpha \right)\]. Gọi M và N lần lượt là trung điểm của các cạnh SC và SD. Tìm giao điểm P của đường thẳng BN với mặt phẳng (SAC).

Lời giải

Ta có:

• (SBD)\[\supset \]BN

• (SBD)\[\cap \] (SAC)=SO

• Trong mp(SBD), gọi \[P\in SO\cap BN\]

\[\Rightarrow P=BN\cap (SAC)\]

Vậy P là giao điểm cần tìm.

Giải thích