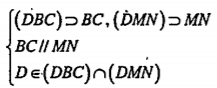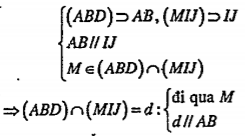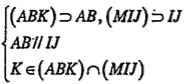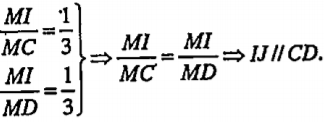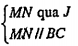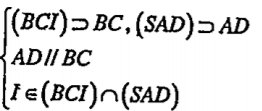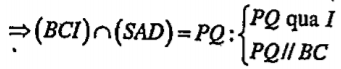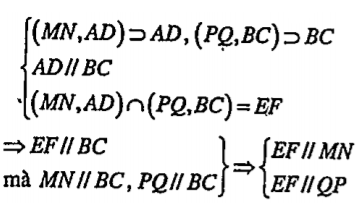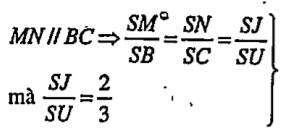C. CÂU HỎI VÀ BÀI TẬP
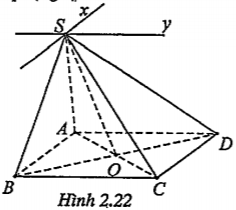
Bài 2.10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các cặp mặt phẳng sau đây:
a) (SAC) và (SBD).
b) (SAB) và (SCD)
c) (SAD) và (SBC)
| Lời giải a) Giao tuyến của (SAC) và (SBD) Gọi O=AC\[\cap \]BD thì SO=(SAC)\[\cap \] (SBD) | Giải thích Tìm hai điểm chung của hai mặt phẳng. |
| b) Giao tuyến của (SAB) và (SCD) \[(SAB)\supset AB\] \[(SCD)\supset CD\] \[AB//CD\] \[S\in (SAB)\cap (SCD)\] \[\Rightarrow (SAB)\cap (SCD)=Sx(Sx//AB)\] | Áp dụng định lý 2.
|
| c) Giao tuyến của (SAD) và (SBC) Tương tự , ta có: (SAD)\[\cap \] (SBC)=Sy (Sy//AD) | Áp dụng định lý 2. |
Bài 2.11. Cho tứ diện ABCD. Trên các cạnh AB, AC lần lượt lấy các điểm M và N sao cho \[\frac{AM}{AB}=\frac{AN}{AC}\]. Tìm giao tuyến của hai mặt phẳng (DBC) và (DMN).
| Lời giải Vì \[\frac{AM}{AB}=\frac{AN}{AC}\] nên MN // BC. Ta có:
\[\Rightarrow (DBC)\cap (DMN)=Dt,Dt//BC\] | Giải thích Áp dụng định lí Thales đảo cho mặt phẳng (ABC), ta có MN//BC.
|
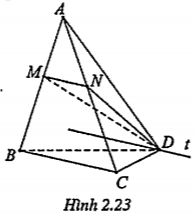
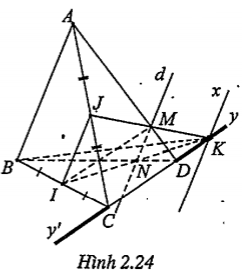
Bài 2.12. Cho tứ diện ABCD. Cho I, J tương ứng là trung điểm của BC và AC. M là một điểm tùy ý trên cạnh AD.
a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD).
b) Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và JM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không là trung điểm của AD).
c) Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ)
| Lời giải a) Giao tuyến của (MIJ) và (ABD) Та сó
| Giải thích Áp dụng hệ quả của định lý 2 Vì IJ là đường trung bình của tam giác ABC nên IJ//AB.
|
| b) Tập hợp của K Ta có: \[K\in IN,IN\subset (BCD)\Rightarrow K\in (BCD)\] (1) \[K\in JM,JM\subset (ACD)\Rightarrow K\in (ACD)\] (2) (1) và (2)\[\Rightarrow \] K\[\in \] (BCD)\[\cap \] (ACD) (3) Mặt khác:(BCD)\[\cap \] (ACD)=CD (4) (3) và (4)\[\Rightarrow K\in CD\]. Do đó khi M chạy trên AD thì K chạy trên hai đường thẳng CD. Giới hạn: Khi M trùng với trung điểm của AD thì JM//IN // CD nên không có điểm K. Vậy tập hợp của K là hai nửa đường thẳng Dy và Cy’. | Hướng dẫn: Hãy chứng minh K thuộc giao tuyến của hai mặt phẳng (ACD) và (BCD).
|
| c) Giao tuyến của (ABK) và (MIJ) Ta có:
\[\Rightarrow (ABK)\cap (MIJ)=Kx\] với Kx//AB | Áp dụng hệ quả của định lí 2. |
Bài 2.13. Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MPNQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ, RS cắt nhau tại trung điểm của mỗi đoạn.
| Lời giải Đề nghị độc giả xem bài tương tự tại ví dụ của vấn đề 2. |
|
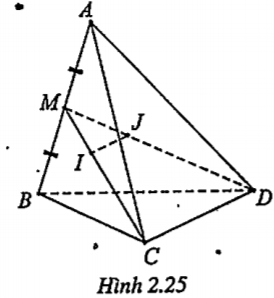
Bài 2.14. Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng IJ//CD.
| Lời giải Gọi M là trung điểm của AB, thì \[I\in CM,J\in DM\] Vì I,J là trọng tâm của \[\Delta \]ABC và \[\Delta \]ABD nên ta có:
| Giải thích Để ý rằng hai tam giác ABC và ABD có cạnh AB chung nên ta chọn M là trung điểm của AB. Trong tam giác MCD, ta chứng minh IJ//CD (bằng tính chất trọng tâm của tam giác).
|
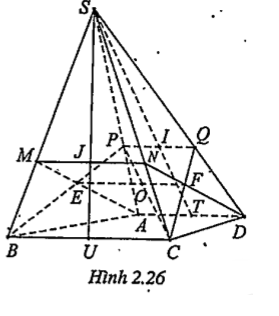
Bài 2.15. Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy là AD và BC. Biết AB = a, BC = b. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC tại M, N. Mặt phẳng (BCI) cắt SA, SD lần lượt tại P và Q.
a) Chứng minh MN song song với PC.
b) Giả sử AM cắt BP tại E, CQ cắt DN tại F. Chứng minh rằng EF song song với MN và PQ. Tính EF theo a và b.
| Lời giải a) Chứng minh MN // PQ Ta có: (ADJ)\[\supset \] AD, (SDC)\[\supset \] BC AD//BC J\[\in \] (ADJ)\[\cap \] (SBC) \[\Rightarrow \] (ADJ)\[\cap \] (SBC)=MN: | Hướng dẫn Áp dụng hệ quả của định 2.
|
| Tương tự :
Vậy: MN//PQ vì cùng song song với BC. |
|
| b) Chứng minh EF//MN và EF//PQ Ta có:
• Tính EF Gọi U và T lần lượt là trung điểm của BC và AD. Ta có:
\[\Rightarrow \frac{SM}{SB}=\frac{SN}{SC}=\frac{2}{3}\] (1) Tương tự: \[\frac{SP}{SA}=\frac{SQ}{SD}=\frac{2}{3}\] (2) (1) và (2) \[\Rightarrow \frac{SM}{SB}=\frac{SP}{SA}\]\[\Rightarrow \] MP//AB \[\Rightarrow \frac{MP}{AB}=\frac{SM}{SB}=\frac{2}{5}\] Mặt khác: \[\frac{MP}{AB}=\frac{EP}{EB}\Rightarrow \frac{2}{3}=\frac{EP}{EP+EB}\Rightarrow \frac{EP}{BP}=\frac{2}{5}\] Gọi \[O\in CP\cap EF\], ta có \[EO//BC\Rightarrow \frac{EP}{BP}=\frac{EO}{BC}\Rightarrow \frac{2}{5}=\frac{EO}{BC}\] | Áp dụng hệ quả của định lý 2.
• Nhắc lại tính chất của tỉ lệ thức: Nếu \[\frac{a}{b}=\frac{c}{d}\]thì \[\frac{a}{a+b}=\frac{c}{c+d}\] |
| \[\Rightarrow EO=\frac{2}{5}BC\Rightarrow EO=\frac{2}{5}b\] (3) Tương tự, ta có: \[\frac{FQ}{CN}=\frac{2}{3}\Rightarrow \frac{CQ}{CF}=\frac{5}{3}\] \[\frac{CF}{CQ}=\frac{FO}{FQ}\Rightarrow \frac{FO}{FQ}=\frac{3}{5}\Rightarrow FO=\frac{3}{5}FQ\] \[\Rightarrow FO=\frac{3}{5}.\frac{2}{3}AD\Rightarrow FO=\frac{2}{5}a\] (4) (3)+(4): \[EO+FO=\frac{2}{5}b+\frac{2}{5}a\] Vậy \[EF=\frac{2}{5}\left( a+b \right)\] | • Biến đổi: (1),(2) \[\Rightarrow \frac{SN}{SC}=\frac{SQ}{SD}\Rightarrow NQ//CD\] \[\Rightarrow \frac{NQ}{CD}=\frac{SQ}{SD}=\frac{2}{3}\] Mặt khác \[\Rightarrow \frac{FQ}{CF}=\frac{NQ}{CD}\Rightarrow \frac{FQ}{CF}=\frac{2}{3}\] \[\Rightarrow \frac{FQ+CF}{CF}=\frac{5}{3}\Rightarrow \frac{CF}{CQ}=\frac{3}{5}\] |