B. DẠNG TOÁN CƠ BẢN
Vấn đề 1. Xác định ảnh của một hình qua phép đối xứng tâm
1. Phương pháp
Để xác định ảnh của một hình qua phép đối xứng tâm I, ta có thể dùng các phương pháp sau:
• Dùng định nghĩa của phép đối xứng tâm.
• Dùng biểu thức tọa độ của phép đối xứng tâm:
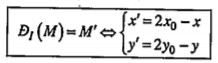
• Dùng tính chất của phép đối xứng tâm.
2. Ví dụ
Ví dụ 1. Trong mặt phẳng Oxy cho điểm M(-1;2), đường thẳng d: x-2y-2=0 và đường tròn (C):\[{{x}^{2}}+{{y}^{2}}+6x-8y=0\]. Tìm ảnh M’, d’, (C') của M, d và (C) qua phép đối xứng tâm O.
| Lời giải • Ta có:
| Giải thích Dùng biểu thức tọa độ của phép đối xứng tâm O(0;0) Chú ý. Hai điểm (không trùng với gốc tọa độ) đối xứng nhau qua gốc tọa độ thì hoành độ và tung độ của chúng đối nhau.
|
| • Lấy A(2;0)\[\in \] d. Gọi Ta có:
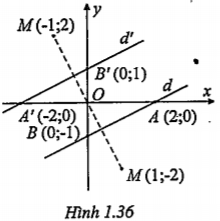
Vậy d’: x-2y+2=0 Cách khác (H.1.36)
| Các bước thực hiện: • Lấy điểm A bất kì trên d (thường lấy giao điểm của d với hai trục tọa độ). • Tìm ảnh A’ của A qua phép đối xứng tâm O. • Viết phương trình đường thẳng d’ ảnh của d qua phép đối xứng tâm O.
|
| Gọi \[A\in d\cap Ox\Rightarrow A(2;0)\] \[B\in d\cap Oy\Rightarrow B(0;-1)\] Ta có:
Đường thẳng d’ đi qua A’B’
\[\Rightarrow \]d’: x-2y+2=0 | Đó là đường thẳng cần tìm
|
| • Đường tròn (C) có: Gọi I’(x’;y’)= Vậy (C’): \[{{(x-3)}^{2}}+{{(y+4)}^{2}}=25\] | Các bước thực hiện: • Xác định tâm và bán kính R của (C) • Tìm I’ ảnh của I qua phép đối xứng tâm O. • Viết phương trình đường tròn (C’) có tâm và bán kính đã biết
|
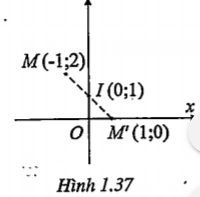
Ví dụ 2. Trong mặt phẳng Oxy cho hai điểm M(-1;2), I(0;1) và đường thẳng d: x-2y-2=0. Tìm ảnh M’, d’ của M và d qua phép đối xứng tâm I.
| Lời giải • Ta có:
• Gọi \[A\in d\cap Ox\Rightarrow A(2;0)\] Ta có:
| Giải thích Dùng biểu thức tọa độ của phép đối xứng tâm I.
|
| Cách dựng: • Vì Suy ra: \[A\in d'\cap (C)\] • Dựng Vậy ABCD là hình bình hành cần dựng. Chứng minh: ABCD là hình bình hành vì có hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường. Ngoài ra, đỉnh C thuộc d, đỉnh A thuộc (C). Biện luận: Số nghiệm hình của bài toán phụ thuộc vào số giao điểm của d’ và (C). • Nếu d’ và (C) có 2 giao điểm thì bài toán có hai nghiệm hình. • Nếu d’ và (C) có 1 giao điểm thì bài toán có một nghiêm hình duy nhất. • Nếu d’ và (C) không có điểm chung thì bài toán không có nghiệm hình.
|
|

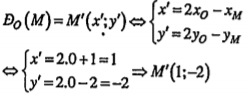
.png) thì A’(-2;0).
thì A’(-2;0)..png)
.png) =A’(-2;0),
=A’(-2;0), .png) =B’(0;1)
=B’(0;1)
.png)
.png) thì I’(3;-4)
thì I’(3;-4)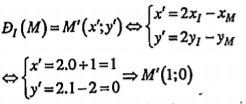
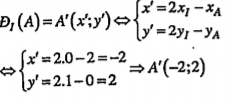
.png) và C\[\in \]d nên A\[\in \]d' là ảnh của d qua phép
và C\[\in \]d nên A\[\in \]d' là ảnh của d qua phép .png)
.png)
.png)