C. CÂU HỎI VÀ BÀI TẬP
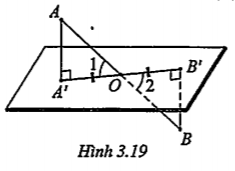
Bài 3.16. Một đoạn thẳng AB không vuông góc với mặt phẳng (α) cắt mặt phẳng này tại trung điểm O của đoạn thẳng đó. Các đường thẳng vuông góc với (α) qua A và B lần lượt cắt mặt phẳng (α) tại A' và B'.
Chứng minh ba điểm A', O, B' thẳng hàng và AA' = BB'
| Lời giải Ta có: \[AA'\bot \left( \alpha \right),BB'\bot \left( \alpha \right)\Rightarrow AA'//BB'\] \[\Rightarrow \exists \left( AA',BB' \right)\] \[\left( AA',BB' \right)\cap \left( \alpha \right)=A'B'\] (1) mà \[O\in AB\cap \left( \alpha \right)\] nên \[O\in A'B'\]
(1) và (2) cho ta A’, O và B' thẳng hàng. Trong mặt phẳng (AA', BB’), hai tam giác vuông OA'A và OB’B có: OA'=OB’ \[\widehat{{{O}_{1}}}=\widehat{{{O}_{2}}}\] (đối đỉnh) nên \[\Delta \]OA’A =\[\Delta \]OB’B\[\Rightarrow \]AA' =BB’. | Giải thích Hai đường thẳng song song AA', BB’ xác định duy nhất mặt phẳng (AA',BB').
|
Bài 3.17. Cho tam giác ABC. Gọi (α) là mặt phẳng vuông góc với đường thẳng CA tại A và (β) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng (α) và (β) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC).
| Lời giải • Chứng minh (α) cắt (β) Giả sử (α) //(β), khi đó: CA\[\bot \] (α) CB\[\bot \] (β) (α) //(β) \[\Rightarrow \]CA//CB: vô lí vì ABC là một tam giác. Như vậy (α) và (β) không thể song song nhau. Giả sử (α)\[\equiv \] (β), khi đó từ một điểm C ta kẻ được hai đường thẳng CA và CB cùng vuông góc với (α): vô lí. Vậy (α) và (β) không thể trùng nhau. Vậy (α) và
| Giải thích Ta chứng minh hai mặt phẳng (α) và (β) cắt nhau bằng phản chứng. Chú ý rằng hai mặt phẳng có ba vị trí tương đối. Nếu cả hai trường hợp song song và trùng nhau không xảy ra thì hai mặt phẳng đó phải cắt nhau.
|
| • Chứng minh d\[\bot \] (ABC) Ta có:
| Ta chứng minh d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (ABC). |
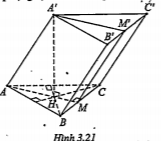
Bài 3.18. Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi H là trực tâm của tam giác ABC và biết rằng A'H vuông góc với mặt phẳng (ABC). Chứng minh rằng:
a) AA' ⊥ BC và AA' ⊥ B'C'.
b) Gọi MM' là giao tuyến của mặt phẳng (AHA') với mặt bên BCC'B', trong đó M ∈ BC và M' ∈ B'C'. Chứng minh rằng tứ giác BCC'B là hình chữ nhật và MM' là đường cao của hình chữ nhật đó.
| a) Chứng minh AA'\[\bot \]BC, AA' \[\bot \]B’C’ Ta có: AH :hình chiếu của AA' trên (ABC) BC\[\bot \]AH \[\Rightarrow \]BC\[\bot \]AA' mà B'C'//BC \[\Rightarrow \]AA' \[\bot \]B'C'. Vậy: AA' \[\bot \]BC và AA' \[\bot \]B’C’ | Giải thích Áp dụng định lí ba đường vuông góc
|
| b) Chứng minh BCC'B' là hình chữ nhật Ta có: AM =(AHA')\[\cap \] (ABC) AH\[\in \] (AHA')\[\cap \] (ABC) Suy ra H\[\in \]AM Khi đó (AHA’)\[\equiv \] (AMM'A’) BC\[\bot \]AM BC\[\bot \]AA’ ⇒ BC\[\bot \](AMM'A') \[\Rightarrow \]BC\[\bot \]MM’ (1) Tứ giác AMM’A’ là hình bình hành nên MM'//BB' (2) (1) và (2)\[\Rightarrow \] BC\[\bot \]BB'. Vậy BCC’B’ là hình chữ nhật vì nó là hình bình hành có hai cạnh BC và BB’ vuông góc. Ngoài ra, MM’ là đường cao của hình chữ nhật đó. | Chú ý rằng BCC'B' là hình bình hành. Nó trở thành hình chữ nhật khi có hai cạnh BC và BB' vuông góc.
|
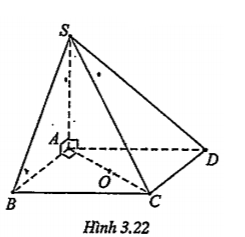
Bài 3.19. Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là điểm đối xứng của của điểm B qua trung điểm O của cạnh AC. Chứng minh rằng CD ⊥ CA và CD ⊥ (SCA).
| Lời giải • Chứng minh CD⊥CA Ta có: AB⊥CA (1) mà CD//AB (2) (1) và (2)\[\Rightarrow \] CD⊥CA.
| Giải thích Ta chứng minh AB⊥CA. Chú ý rằng một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
|
| Ta có: AB⊥ (SAC) mà CD // AB \[\Rightarrow \]CD⊥ (SAC) | Chú ý rằng nếu đường thẳng a vuông góc với mặt phẳng (P) và a//b thì đường thẳng b cũng song song với (P)
|
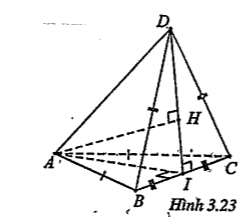
Bài 3.20. Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng khác nhau có chung cạnh đáy BC tạo nên tứ diện ABCD. Gọi I là trung điểm của cạnh BC.
a) Chứng minh BC ⊥ AD
b) Gọi AH là đường cao của tam giác ADI. Chứng minh rằng AH vuông góc với mặt phẳng (BCD).
| a) Chứng minh BC ⊥ AD \[\Delta \]ABC cân tại A nên trung tuyến AI cũng là đường cao: BC⊥AI (1) \[\Delta \]DBC cân tại D nên trung tuyến DI cũng là đường cao: BC⊥DI (2) (1) và (2) suy ra: BC⊥ (ADI)\[\Rightarrow \] BC⊥AD. | Ta chứng minh BC vuông góc với mặt phẳng (ADI).
|
| b) Chứng minh AH vuông góc với mặt phẳng (BCD) Та сó: BC ⊥ (ADI) (ADI)\[\supset \] AH =>BC ⊥AH mà AH ⊥DI => AH ⊥ (BCD). | Ta chứng minh AH vuông góc với hai đường thẳng DI và BC cắt nhau trong mặt phẳng (BCD). |
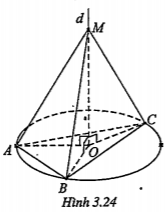
Bài 3.21. Chứng minh rằng tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó.
| Lời giải Phần thuận • Giả sử MA = MB=MC. Gọi O’ là hình chiếu của M trên (\[\alpha \]). • Xét ba tam giác O’AM,O'BM và O’CM , ta có: O’M chung
MA=MB = MC \[\Rightarrow \]\[\Delta \]O'AM= \[\Delta \]O'BM = \[\Delta \]O'CM \[\Rightarrow \]O'A=O'B=O'C \[\Rightarrow \]O'=O \[\Rightarrow \]MO\[\bot \] (\[\alpha \]) \[\Rightarrow \]M\[\in \]d Vậy nếu M cách đều ba đỉnh của \[\Delta \]ABC thì nằm trên d Phần đảo Giả sử M\[\in \]d thì \[\Delta \]O'AM= \[\Delta \]O'BM = \[\Delta \]O'CM (c-g-c) nên MA = MB=MC. Vậy nếu M thuộc d thì M cách đều ba đỉnh của tam giác đó. | Giải thích
Chú ý. Đường thẳng d nói trên được gọi là trục của đường tròn ngoại tiếp tam giác ABC. |

.png) cắt nhau theo giao tuyến d.
cắt nhau theo giao tuyến d.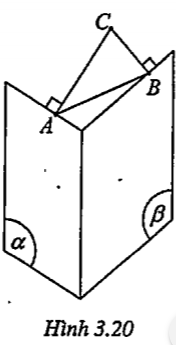
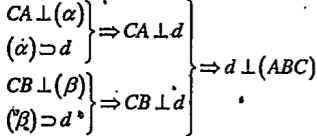
.png)