Vấn đề 4. Dùng phép đồng dạng để chứng minh hai hình đồng dạng
1. Phương pháp
Ta chứng minh có một phép đồng dạng biến hình này thành hình kia.
2. Ví dụ.
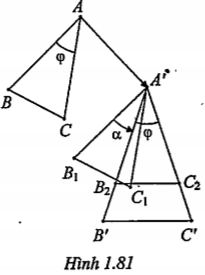
Ví dụ. Chứng minh rằng các tam giác cân có số đo của góc ở đỉnh bằng nhau thì đồng dạng
| Lời giải Giả sử có hai tam giác cân tại A và A’ là ABC và A’B’C' cùng có số đo của góc ở đỉnh là \[\varphi \]. Ta có • Phép tịnh tiến \[{{T}_{\overrightarrow{AA'}}}\] đã biến tam giác ABC thành tam giác | Giải thích Cần chú rằng khi thực hiện phép quay |
..png)
với \[\alpha =(A'{{B}_{1}},A'B')\] biến tam giác .png)
thành tam giác .png)
ta có .png)
//B’C’
| • Phép quay • Phép vị tự Vậy phép đồng dạng có được bằng cách thực hiện liên tiếp các phép \[{{T}_{\overrightarrow{AA'}}}\], |
|
.png)
, với \[\alpha \]=(.png)
,A’B’) biến tam giác .png)
thành tam giác .png)
..png)
với \[k=\frac{B'A'}{BA}\]biến tam giác .png)
thành tam giác A'B'C’..png)
biến tam giác ABC thành tam giác A’B’C’ nên chúng đồng dạng với nhau.