Dạng bài tập ở cấp độ thông hiểu yêu cầu học sinh áp dụng thành thạo các công thức và bước đầu biết phát hiện một số tính chất hình học đơn giản để giải quyết các tình huống cụ thể.
Ví dụ 5.3. Cho tứ diện ABCD có cạnh \[AD=a\sqrt{2}\], các cạnh còn lại bằng a. Diện tích mặt cầu ngoại tiếp tứ diện là
A. \[2\pi {{a}^{2}}\].
B. \[\pi {{a}^{2}}\]
C. \[4\pi {{a}^{2}}\].
D. \[8\pi {{a}^{2}}\].
Phân tích: Bài toán này, với cách giải quyết theo hướng “tự luận” quen thuộc, chúng ta thường làm như sau:
Bước 1: Xác định trục đường tròn ngoại tiếp đa giác đáy.
Bước 2: Xác định mặt phẳng trung trực của một cạnh bên (hoặc đường trung trực của cạnh bên đồng phẳng với trục đường tròn đáy). Giao điểm của trục đường tròn đáy với mặt phẳng trung trực (hoặc đường trung trực của cạnh bên) là tâm mặt cầu ngoại tiếp khối chóp.
Bước 3: Tính khoảng cách từ tâm đến một đỉnh tùy ý ta có bán kính mặt cầu, từ đó sẽ tính được diện tích của mặt cầu.
Tuy nhiên với cách tiếp cận theo hướng “trắc nghiệm”, trong bài toán này, chúng ta chỉ cần biết tính chất: Trong tam giác vuông, trung điểm của cạnh huyền cách đều các đỉnh, thì việc xác định tâm của mặt cầu sẽ đơn giản và nhanh hơn, cụ thể như sau:
Hướng dẫn giải
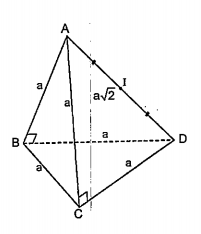
Dễ thấy các tam giác ABD và ACD vuông tại B và C.
Gọi I là trung điểm của AD.
\[\Rightarrow \] I cách đều A, B, C, D
\[\Rightarrow \] I là tâm mặt cầu ngoại tiếp tứ diện ABCD.
\[\Rightarrow R=\frac{AD}{2}=\frac{a\sqrt{2}}{2}.\]
Vậy diện tích mặt cầu là:
\[S=4\pi {{R}^{2}}=2\pi {{a}^{2}}.\]
Vậy phương án đúng là A.
Ví dụ 5.4. Cho hình lăng trụ ABC.A'B'C'. Diện tích tứ giác ABB'A' bằng 24 cm. Khoảng cách từ đường thẳng CC' đến mặt phẳng (ABBA) là 6 cm. Thể tích lăng trụ ABC.A'B'C' là
A.216 (cm3).
B. 36 (cm3).
C. 72 (cm3).
D. \[\frac{216}{5}\] (cm3).
Phân tích: Phương pháp chung để tính thể tích lăng trụ là chúng ta cần tính chiều cao và diện tích đáy. Với bài toán này các dữ kiện đã cho không thuận lợi theo hướng đó. Tuy nhiên, nếu chú ý đến tính chất sau, chúng ta sẽ có lời giải khá dễ dàng:
– Một hình chóp có đỉnh thuộc một mặt đáy của lăng trụ và có đáy trùng với đáy còn lại của lăng trụ đó thì thể tích khối chóp đó bằng \[\frac{1}{3}\] thể tích khối lăng trụ.
- Nếu hình chóp có đỉnh thuộc một mặt đáy của lăng trụ, còn mặt đáy là mặt bên của lăng trụ thì thể tích của khối chóp đó bằng \[\frac{2}{3}\] thể tích khối lăng trụ.
Hướng dẫn giải
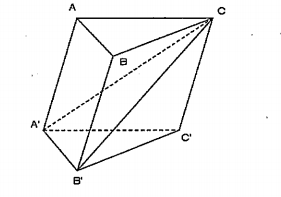
Ta có \[{{V}_{ABC.A'B'C'}}={{V}_{C.ABB'A'}}+{{V}_{C.A'B'C'}}={{V}_{C.ABB'A'}}+\frac{1}{3}{{V}_{ABC.A'B'C'}}\]
\[\Rightarrow \frac{2}{3}{{V}_{ABC.A'B'C'}}={{V}_{C.ABB'A'}}\]
\[\Rightarrow {{V}_{ABC.A'B'C'}}=\frac{3}{2}{{V}_{C.ABB'A'}}=\frac{3}{2}.\frac{1}{3}d(C,(ABB'A')).{{S}_{ABB'A'}}=\frac{1}{2}d(CC',(ABB'A')).{{S}_{ABB'A'}}=\frac{1}{2}.6.24=72\](cm3)
Vậy C là đáp án đúng.
