Chuyên đề 4: SỐ PHỨC

4.1. TÓM TẮT LÍ THUYẾT

4.1.1. Số phức

4.1.1.1. Số i

Ta đưa ra một số mới, kí hiệu là i thoả mãn . Khi đó i là một nghiệm của phương trình x2 + 1 = 0.

4.1.1.2. Định nghĩa số phức

Định nghĩa 4.1. Một số phức là một biểu thức dạng a + bi, trong đó \[a,b\in \mathbb{R}\] và số i thoả mãn \[{{i}^{2}}=-1\]. Kí hiệu số phức đó là z và viết z = a + bi, i được gọi là đơn vị ảo, a được gọi là phần thực và b được gọi là phần ảo của z.

Tập hợp các số phức kí hiệu là \[\mathbb{C}\].

Chú ý 4.1.

- Số phức z = a + 0i có phần ảo bằng 0, là số thực. Vậy ta có \[\mathbb{R}\subset \mathbb{C}\].

- Số phức z = 0 + bi (\[b\in \mathbb{R}\]) có phần thực bằng 0 được gọi là số ảo hay số thuần ảo. Đặc biệt, i=0+ li là một số ảo.

4.1.1.3. Số phức bằng nhau

Định nghĩa 4.2. Hai số phức z = a + bi (\[a,b\in \mathbb{R}\]) và z' = a’ + b'i (\[a,b\in \mathbb{R}\]) được gọi là bằng nhau nếu và viết z = z’.

4.1.1.4. Biểu diễn hình học số phức

Trong mặt phẳng toạ độ Oxy. Mỗi số phức z = a + bi (\[a,b\in \mathbb{R}\]) được biểu diễn bởi điểm M có toạ độ (a;b). Ngược lại, mỗi điểm M(a;b) biểu diễn số phức z = a + bi. Ta còn viết M(a + bi) hay M(z).

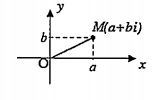
Mặt phẳng toạ độ với việc biểu diễn các số phức như trên được gọi là mặt phẳng phức.

Chú ý 4.2.

- Gốc toạ độ O biểu diễn số 0;

- Các điểm trên trục hoành biểu diễn các số thực, nên trục Ox được gọi là trục thực;

- Các điểm trên trục tung Oy biểu diễn các số ảo, do đó trục Oy còn được gọi là trục ảo.

4.1.1.5. Số phức liên hợp

Định nghĩa 4.3. Số phức liên hợp của số phức z = a + bi(\[a,b\in \mathbb{R}\]) là số phức a – bi và được kí hiệu là \[\overline{z}\]. Như vậy \[\overline{z}\] = a - bi.

Chú ý 4.3.

– Ta có \[\overline{\overline{z}}\]=z nên ta nói z và \[\overline{z}\] là hai số phức liên hợp với nhau.

- Hai số phức là liên hợp với nhau khi và chỉ khi các điểm biểu diễn của chúng đối xứng với nhau qua trục Ox.

4.1.1.6. Môđun của số phức

Định nghĩa 4.4. Môđun của số phức z = a + bi (\[a,b\in \mathbb{R}\]) là số thực không âm \[\sqrt{{{a}^{2}}+{{b}^{2}}}\] và được kí hiệu là \[\left| z \right|\].

Như vậy nếu z = a + bi (\[a,b\in \mathbb{R}\]) thì \[\left| z \right|=\left| a+bi \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\].

Chú ý 4.4

\[\left| z \right|=\left| \overline{OM} \right|=OM\] là điểm biểu diễn số phức z.

Với mọi \[z\in \mathbb{C}\] ta có \[\left| z \right|=\left| \overline{z} \right|\];

Nếu z là số thực thì môđun của z là giá trị tuyệt đối của số thực đó.