Chuyên đề 5
HÌNH HỌC KHÔNG GIAN
5.1. TÓM TẮT LÍ THUYẾT
5.1.1. Thể tích khối đa diện
Thể tích khối chóp: \[V=\frac{1}{3}h{{S}_{đ}}\], trong đó h và Sđ lần lượt là chiều cao và diện tích đáy của khối chóp.
Thể tích khối lăng trụ: y = hSđ, trong đó h và Sđ lần lượt là chiều cao và diện tích đáy của khối lăng trụ.
5.1.2. Tỉ số thể tích khối chóp
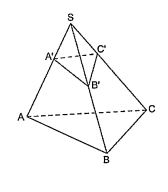
Mặt phẳng (P) cắt các cạnh SA, SB, SC của khối chóp S.ABC tại A', B', C'. Khi đó ta có:
\[\frac{{{V}_{S.A'B'C'}}}{{{V}_{S.ABC}}}=\frac{SA'.SB'.SC'}{SA.SB.SC}\]
5.1.2. Thể tích khối tròn xoay
Cho khối cầu có bán kính R, khi đó:
Thể tích khối cầu: \[V=\frac{4}{3}\pi {{R}^{3}}\].
Diện tích mặt cầu: \[S=4\pi {{R}^{2}}\].
Cho khối nón tròn xoay có chiều cao h, bán kính đáy R và độ dài đường sinh l. Khi đó:
Thể tích khối nón V = \[\frac{1}{3}\]hSđ = \[\frac{1}{3}h\pi {{R}^{2}}\].
Diện tích xung quanh \[{{S}_{xq}}=l\pi R.\]
Diện tích toàn phần Stp = Sxq + Sđ = \[l\pi R+\pi {{R}^{2}}\].
Cho khối trụ tròn xoay có chiều cao h và bán kính đáy R. Khi đó:
Thể tích khối trụ: V = hSđ = \[h\pi {{R}^{2}}\].
Diện tích xung quanh Sxq = \[h2\pi R\].
Diện tích toàn phần Stp = Sxq + 2Sđ = \[2\pi Rh+2\pi {{R}^{2}}.\]
