3.2. NHỮNG DẠNG TOÁN THƯỜNG GẶP
Phương pháp (khi làm bài trắc nghiệm)
+ Cách 1. Phân tích \[y=f(x)\] thành tổng của các hàm số thường gặp. Áp dụng các tính chất và bảng nguyên hàm cơ bản ta tìm ra họ nguyên hàm của f(x) rồi chọn phương án phù hợp.
+ Cách 2. Ta tiến hành qua các bước:
Bước 1. Đọc lướt đề bài để biết dạng của hàm f từ đó suy ra dạng của nguyên hàm F của nó. Tìm trong số các phương án đã cho những phương án có nhiều khả năng là phương án đúng đồng thời loại bỏ những phương án không thể.
Bước 2. Đọc kĩ hàm f và các phương án còn lại để tìm ra sự khác nhau giữa các phương án và đối chiếu với dạng nguyên hàm có thể có của hàm số f(x) để loại tiếp đi những phương án không phù hợp.
Bước 3. Đạo hàm lần lượt các phương án khả dĩ nhất trong số các phương án còn lại và đối chiếu với hàm \[f(x)\] để chọn phương án đúng.
Ví dụ 3.1. Nguyên hàm của hàm số \[f(x)={{({{x}^{2}}-1)}^{2}}\] là
A. \[\frac{{{x}^{5}}}{5}-\frac{2{{x}^{3}}}{3}+x+C.\]
B. \[\frac{{{x}^{5}}}{5}+\frac{2{{x}^{3}}}{3}+x+C.\]
C. \[\frac{{{x}^{4}}}{4}-\frac{2{{x}^{3}}}{3}+x+C.\]
D. \[\frac{{{x}^{5}}}{5}-\frac{2{{x}^{3}}}{3}+x+\ln \left| x \right|+C.\]
Hướng dẫn giải
Ta có \[f(x)={{x}^{4}}-2{{x}^{2}}+1\]
Áp dụng các tính chất của nguyên hàm và sử dụng bằng nguyên hàm cơ bản ta được
\[\int{f(x)dx=\int{({{x}^{4}}-2{{x}^{2}}+1)dx=\int{{{x}^{4}}dx-\int{2{{x}^{2}}dx+\int{1dx}}}}}\]
=\[\frac{{{x}^{5}}}{5}-\frac{2{{x}^{3}}}{3}+x+C.\]
Vậy ta chọn phương án A.
Bước 1. Ta thấy \[f(x)\] là một đa thức nên nguyên hàm của nó cũng phải là một đa thức, do đó ta loại phương án D.
Bước 2. Ta thấy các phương án A và B là các đa thức cùng bậc, khác nhau về dấu còn phương án A và C khác nhau về bậc. Mặt khác, f(x) là một đa thức bậc 4 nên nguyên hàm của nó phải là đa thức bậc 5, phương án C là một đa thức bậc 4 nên ta loại C. Do f là bình phương của một hiệu (khi khai triển f có chứa dấu "=") nên nguyên hàm của nó cũng phải chứa dấu "=" do đó ta loại phương án B. Do đó phương án A là phương án đúng.
Nhận xét:
- Với cách 1: Ta phải tiến hành các tính toán cụ thể và thường được sử dụng trong các bài thi tự luận. Ngoài ra, nếu ta coi các phương án đã cho: A, B, C, D là các giả thiết thì Cách 1 chỉ sử dụng các giả thiết này để so sánh với kết quả tìm được khi đã hoàn thành các tính toán, nên chưa sử dụng triệt để các giả thiết dẫn đến thời gian làm bài thường lâu hơn Cách 2.
– Với cách 2:Ta coi mỗi phương án đã cho là các giả thiết cùng với giả thiết của bài toán và sử dụng các lập luận, các tính chất đã biết để đi đến phương án đúng nên thường tốn ít thời gian hơn Cách 1.
Ví dụ 3.2. Phát biểu nào sau đây là đúng?
A. \[\int{(4{{\sin }^{2}}x+{{2}^{x}})dx=2x-\sin 2x+\frac{{{2}^{x}}}{\ln 2}}-C.\]
B. \[\int{(4{{\sin }^{2}}x+{{2}^{x}})dx=2x+\sin 2x+\frac{{{2}^{x}}}{\ln 2}}+C.\]
C. \[\int{(4{{\sin }^{2}}x+{{2}^{x}})dx=\frac{4}{3}{{\sin }^{3}}x+\frac{{{2}^{x}}}{\ln 2}}+C.\]
D. \[\int{(4{{\sin }^{2}}x+{{2}^{x}})dx=2x-\sin 2x+{{2}^{x}}\ln 2}+C.\]
Hướng dẫn giải
\[\int{(4{{\sin }^{2}}x+{{2}^{x}})dx=\int{\text{ }\!\![\!\!\text{ }}2(1-\cos 2x)+{{2}^{x}}]dx=2x-sin2x+\frac{{{2}^{x}}}{\ln 2}}+C.\]
Do đó phương án A là đúng.
- Hàm cần tìm nguyên hàm có chứa hàm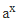 
nên nguyên hàm của nó có chứa \[\frac{{{a}^{x}}}{\ln a}\] vậy ta loại phương án D.
- Ta loại phương án C vì tích phân \[\int{{{\sin }^{2}}xdx}\] không phải ở dạng \[\int{{{u}^{\alpha }}du.}\]
Hai phương án A và B chỉ khác khau về dấu của đại lượng sin2x. Hơn nữa, khi tính tích phân \[\int{{{\sin }^{2u}}xdx}\] ta thường sử dụng công thức hạ bậc để đưa về tích phân dạng \[\int{\operatorname{cosmxdx}}\]. Mà \[{{\sin }^{2}}x=\frac{1-\cos 2x}{2}\], một nguyên hàm của cosx là sinx nên nguyên hàm của sin2x phải chứa dấu (-). Do đó ta chọn phương án A.
Nhận xét: Đây là bài toán ở cấp độ "thông hiểu". Ở Cách 2, bằng cách quan sát kĩ bài toán cùng các phương án trả lời cũng như nắm chắc các tính chất của nguyên hàm, bảng nguyên hàm cơ bản và đặc điểm của hàm cần tìm nguyên hàm ta có thể lựa chọn được phương án đúng mà không cần phải tiến hành các tính toán chi tiết như Cách 1.
Ví dụ 3.3. Nguyên hàm F(x) của hàm số \[f(x)={{(\tan x+2\operatorname{cotx})}^{2}}\] thoả mãn \[F(\frac{\pi }{4})=-\frac{\pi }{4}\] là
A. \[\tan x-4\cot x-x+3.\]
B. \[4\tan x-\cot x-x-3.\]
C. \[2\tan x-2\cot x+x-\frac{\pi }{2}.\]
D. \[\frac{{{(\tan x+2\cot x)}^{3}}}{3}.\]
Hướng dẫn giải
\[\int{{{(\tan x+2\cot x)}^{2}}dx=\int{({{\tan }^{2}}x+4+4{{\cot }^{2}}x)dx=\int{(\frac{1}{{{\cos }^{2}}x}+\frac{4}{{{\sin }^{2}}x}-1)dx=\tan x-4\cot x-x+C}}}\]
\[F(\frac{\pi }{4})=-\frac{\pi }{4}\] khi và chỉ khi \[1-4-\frac{\pi }{4}+C=-\frac{\pi }{4}\] hay C = 3. Vậy ta chọn A.
Thay \[x=\frac{\pi }{4}\] lần lượt vào các phương án trên ta được:
\[-\frac{\pi }{4};-\frac{\pi }{4};-\frac{\pi }{4}\] và 9.
Vậy ta loại phương án D.
Đạo hàm phương án B ta được:
\[\frac{4}{{{\cos }^{2}}x}+\frac{1}{{{\sin }^{2}}x}-1=4{{\tan }^{2}}x+4+{{\cot }^{2}}x={{(2\tan x+\cot x)}^{2}}\].
Đạo hàm phương án C ta được:
\[\frac{2}{{{\cos }^{2}}x}+\frac{2}{{{\sin }^{2}}x}+1=2{{\tan }^{2}}x+5+2{{\cot }^{2}}x.\]
Đạo hàm phương án A ta được:
\[\frac{1}{{{\cos }^{2}}x}+\frac{4}{{{\sin }^{2}}x}-1={{\tan }^{2}}x+4+4{{\cot }^{2}}x={{(\tan x+2\cot x)}^{2}}.\]
Vậy ta chọn A.
Nhận xét: Bài toán ở ví dụ này được xét ở cấp độ "vận dụng thấp". Để giải được bài toán này học sinh cần nắm được các tính chất của nguyên hàm, tính được nguyên hàm (hoặc đạo hàm) của hàm lượng giác cũng như biết cách xác định giá trị của hằng số C.