Ví dụ 1.17. Một chất điểm chuyển động theo quy luật \[s=3{{t}^{2}}-2{{t}^{3}}\]. Thời điểm t (giây) tại đó vận tốc của chuyển động đạt giá trị lớn nhất là:
A. t = 1 (giây). B. t = \[\frac{1}{2}\] (giây). C. t = 2 (giây). D. t = \[\frac{3}{2}\] (giây).
Hướng dẫn giải
Từ phương trình chuyển động \[s=3{{t}^{2}}-2{{t}^{3}},t>0\] suy ra vận tốc chuyển động là \[v=s'=6t-6{{t}^{2}}\]. Ta có \[v'=6-12t\Rightarrow v'=0\Leftrightarrow t=\frac{1}{2}.\]
Hàm số đồng biến trên khoảng \[(0;\frac{1}{2})\] và nghịch biến trên \[(\frac{1}{2};+\infty )\]. Do đó vận tốc đạt lớn nhất khi \[t=\frac{1}{2}\]. Vậy chọn phương án B.
Nhận xét: Với bài toán chuyển động, ta nhớ vận tốc chuyển động của chất điểm bằng đạo hàm của quãng đường theo thời gian và gia tốc bằng đạo hàm của vận tốc theo thời gian.
Ví dụ 1.18. Người ta cần xây một bể chứa nước không có nắp dạng hình hộp chữ nhật có thể tích 3,2 khối nước (1 khối = 1000dm3). Biết rằng tỉ số của chiều cao của bể và chiều rộng của đáy bể bằng 2. Hỏi diện tích toàn phần của bể nước là bao nhiêu để khi xây tiết kiệm nguyên vật liệu nhất?
A. 1200 dm2 . B. 1360 dm2 . C. 160 dm2 . D. 1040 dm2.
Hướng dẫn giải
Ta có 3,2 khối = 3200 dm3.
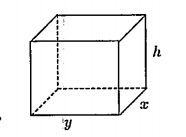
Gọi x,y (dm) (x,y > 0) lần lượt là chiều rộng, chiều dài của đáy bể và h (dm) (h > 0) là chiều cao của bể chứa nước.
Theo giả thiết ta có h = 2x và V = xyh = 3200\[\Rightarrow y=\frac{3200}{hx}=\frac{1600}{{{x}^{2}}}.\]
Ta có diện tích toàn phần của bể chứa nước là
\[S=2xh+2yh+xy=4{{x}^{2}}+\frac{8000}{x}.\]
Khảo sát hàm \[f(x)=4{{x}^{2}}+\frac{8000}{x},x>0\] suy ra diện tích toàn phần nhỏ nhất của bể chứa nước là 1200 dm3 khi x = 10 dm \[\Rightarrow \] y = 16 dm.
Vậy chọn phương án đúng là phương án A.
Nhận xét: Đây là bài toán ứng dụng đạo hàm để giải quyết một tình huống thực tế. Với bài toán này ta hay bị nhầm lẫn diện tích toàn phần S = 2xh + 2y + 2xy, nhưng thực tế bài toán cho cái bể chứa nước không có nắp nên ta phải chọn công thức tính diện tích là S = 2xh + 2yh + xy, từ đó ta đưa về một biến x để khảo sát.
