1.1.5. Khảo sát sự biến thiên và vẽ đồ thị hàm số
1.1.5.1. Các bước khảo sát và vẽ đồ thị hàm số
a) Tìm tập xác định của hàm số.
b) Sự biến thiên:
Chiều biến thiên: Tính y'; tìm các điểm thuộc tập xác định mà tại đó y' bằng 0 hoặc không xác định; xét dấu y' và suy ra các khoảng đồng biến, nghịch biến của hàm số.
- Tìm cực trị.
– Tìm các giới hạn vô cực, các giới hạn tại vô cực và tìm tiệm cận (nếu có).
– Lập bảng biến thiên.
c) Vẽ đồ thị.
1.1.5.2. Các dạng của đồ thị hàm số thường gặp
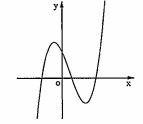
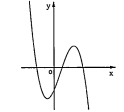
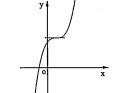
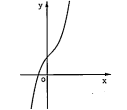
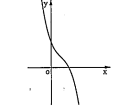
a) Các dạng của đồ thị hàm số bậc ba: \[y=a{{x}^{3}}+b{{x}^{2}}+cx+d(a\ne 0)\].
|
| a>0 | a<0 |
| Phương trình y'=0 có hai nghiệm phân biệt
|
|
|
|
| a > 0 | a < 0 |
| Phương trình \[y'=0\] có nghiệm kép |
|
|
| Phương trình \[y'=0\] vô nghiệm |
|
|
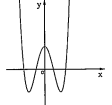
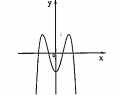
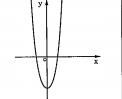
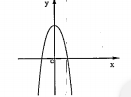
b) Các dạng của đồ thị hàm số bậc bốn: \[y=a{{x}^{4}}+b{{x}^{2}}+c(a\ne 0)\].
|
| a > 0 | a < 0 |
| Phương trình \[y'=0\] có ba nghiệm phân biệt |
|
|
| Phương trình \[y'=0\] có một nghiệm |
|
|
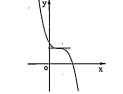
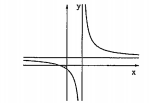
c) Các dạng của đồ thị hàm số phân thức
\[y=\frac{ax+b}{cx+d}(c\ne 0,D=ad-bc\ne 0)\]
| \[D=ad-bc>0\] | \[D=ad-bc<0\] |
|
|
|