Bài toán thuộc dạng này thường nhằm mục đích kiểm tra sự hiểu biết và kĩ năng vận dụng các công thức biến đổi mũ và lôgarit trong việc tính toán, rút gọn biểu thức chứa mũ và lôgarit. Tuỳ thuộc vào các đại lượng đã biết và biểu thức cần tính toán, khai triển, rút gọn mà bài toán sẽ được sắp xếp vào các mức độ phù hợp.
Tương tự như ở Dạng 3, các phương án A, B, C, D đưa ra trong bài toán thường không giúp ta định hướng được theo phương pháp thử chọn. Do đó, các phương án này chỉ đóng vai trò đối chiếu. Chúng ta cần khai triển, rút gọn và tính toán biểu thức để tìm ra được phương án đúng.
Ví dụ 2.9. (Câu 17, Đề minh hoạ môn Toán kì thi THPT Quốc gia năm 2017 của Bộ GD&ĐT)
Cho các số thực dương a, b với \[a\ne 1\]. Khẳng định nào sau đây là khẳng định đúng?
A. \[{{\log }_{{{a}^{2}}}}(ab)=\frac{1}{2}{{\log }_{a}}b.\]
B. \[{{\log }_{{{a}^{2}}}}(ab)=2+2{{\log }_{a}}b.\]
C. \[{{\log }_{{{a}^{2}}}}(ab)=\frac{1}{4}{{\log }_{a}}b.\]
D. \[{{\log }_{{{a}^{2}}}}(ab)=\frac{1}{2}+\frac{1}{2}{{\log }_{a}}b.\]
Phân tích: Quan sát các phương án chúng ta thấy bài toán yêu cầu tìm khai triển đúng cho \[{{\log }_{{{a}^{2}}}}(ab)\] qua \[{{\log }_{a}}(b)\]. Bởi vậy, chúng ta cần vận dụng các công thức hợp lí của lôgarit để tìm được phương án đúng trong bài toán này.
Hướng dẫn giải
Ta có
\[{{\log }_{{{a}^{2}}}}(ab)=\frac{1}{2}{{\log }_{a}}(ab)=\frac{1}{2}({{\log }_{a}}a+{{\log }_{a}}b)=\frac{1}{2}(1+{{\log }_{a}}b)=\frac{1}{2}+\frac{1}{2}{{\log }_{a}}b.\]
Vậy D là phương án đúng.
Nhận xét: Các công thức sử dụng trong ví dụ này là các công thức cơ bản, quá trình biến đổi cũng không "lắt léo". Do đó, bài toán này có thể coi là ở mức độ "thông hiểu".
Bài toán trên có thể sử dụng phương pháp thế một trường hợp riêng của bài toán để kiểm tra kết quả bằng cách ta cho b = a rồi thay vào các phương án ta được:
Với phương án A có \[{{\log }_{{{a}^{2}}}}(ab)=\frac{1}{2}{{\log }_{a}}b\], khi b = a thì \[{{\log }_{{{a}^{2}}}}({{a}^{2}})\ne \frac{1}{2}{{\log }_{a}}a\] nên loại phương án A.
Với phương án B có \[{{\log }_{{{a}^{2}}}}{{a}^{2}}\ne 2+2{{\log }_{a}}a\] nên loại phương án B.
Với phương án C có \[{{\log }_{{{a}^{2}}}}{{a}^{2}}\ne \frac{1}{4}{{\log }_{a}}a\] nên loại phương án C.
Với phương án D có \[{{\log }_{{{a}^{2}}}}{{a}^{2}}=\frac{1}{2}+\frac{1}{2}{{\log }_{a}}a\] nên chọn phương án D.
Ví dụ 2.10. Cho a > 0, \[a\ne 1\]. Khi đó, \[-\frac{1}{2}\] là giá trị của biểu thức nào sau đây?
A. \[{{\log }_{{{a}^{2}}}}a.\]
B. \[{{\log }_{{{a}^{\frac{1}{2}}}}}{{a}^{2}}.\]
C. \[{{\log }_{{{a}^{2}}}}(\frac{1}{a}).\]
D. \[{{\log }_{\sqrt{a}}}a.\]
Phân tích: Tương tự Ví dụ 2.9, chúng ta cần vận dụng các công thức của lôgarit để tìm phương án đúng cho bài toán.
Hướng dẫn giải
Ta có:
A. \[{{\log }_{{{a}^{2}}}}a=\frac{1}{2}{{\log }_{a}}a=\frac{1}{2}.\]
B. \[{{\log }_{{{a}^{\frac{1}{2}}}}}{{a}^{2}}=2{{\log }_{a}}{{a}^{2}}=4{{\log }_{a}}a=4.\]
C. \[{{\log }_{{{a}^{2}}}}\frac{1}{a}=\frac{1}{2}{{\log }_{a}}{{a}^{-1}}=-\frac{1}{2}lo{{g}_{a}}a=-\frac{1}{2}.\]
D. \[{{\log }_{\sqrt{a}}}a={{\log }_{{{a}^{\frac{1}{2}}}}}a=2{{\log }_{a}}a=2.\]
Vậy C là phương án đúng.
Nhận xét:
- Các công thức được vận dụng trong ví dụ này là các công thức cơ bản, quá trình biến đổi cũng không "lắt léo". Do đó, bài toán này có thể coi là ở mức độ "thông hiểu".
- Trong quá trình tính toán, khi gặp phương án nào ra kết quả đúng thì dừng lại và chọn phương án đó.
Ví dụ 2.11. Biểu thức \[{{x}^{\frac{7}{4}}}\], (x > 0) bằng biểu thức nào sau đây?
A. \[\sqrt[3]{{{x}^{5}}\sqrt[4]{x}}\].
B. \[\sqrt[4]{{{x}^{5}}\sqrt[3]{x}}\].
C. \[\sqrt[5]{{{x}^{3}}\sqrt[4]{x}}\].
D. \[\sqrt[3]{{{x}^{4}}\sqrt[5]{x}}\].
Phân tích: Trong ví dụ này, chúng ta cần vận dụng các công thức của luỹ thừa với số mũ nguyên và hữu tỉ để tìm phương án đúng cho bài toán.
Hướng dẫn giải
Ta có:
A. \[\sqrt[3]{{{x}^{5}}\sqrt[4]{x}}={{({{x}^{5}}{{x}^{\frac{1}{4}}})}^{\frac{1}{3}}}={{({{x}^{5+\frac{1}{4}}})}^{\frac{1}{3}}}={{x}^{\frac{1}{3}.\frac{21}{4}}}={{x}^{\frac{7}{4}}}.\]
B. \[\sqrt[4]{{{x}^{5}}\sqrt[3]{x}}={{({{x}^{5}}{{x}^{\frac{1}{3}}})}^{\frac{1}{4}}}={{({{x}^{5+\frac{1}{3}}})}^{\frac{1}{4}}}={{x}^{\frac{1}{4}.\frac{16}{3}}}={{x}^{\frac{4}{3}}}.\]
C. \[\sqrt[5]{{{x}^{3}}\sqrt[4]{x}}={{({{x}^{3}}{{x}^{\frac{1}{4}}})}^{\frac{1}{5}}}={{({{x}^{3+\frac{1}{4}}})}^{\frac{1}{5}}}={{x}^{\frac{1}{5}.\frac{13}{4}}}={{x}^{\frac{13}{20}}}.\]
D. \[\sqrt[3]{{{x}^{4}}\sqrt[5]{x}}={{({{x}^{4}}{{x}^{\frac{1}{5}}})}^{\frac{1}{3}}}={{({{x}^{4+\frac{1}{5}}})}^{\frac{1}{3}}}={{x}^{\frac{1}{3}.\frac{21}{5}}}={{x}^{\frac{7}{5}}}.\]
Vậy A là phương án đúng.
Nhận xét:
- Trong tình huống này, chúng ta hoàn toàn có thể dừng sau khi tính toán xong phương án A. Trong thực tế làm bài, sẽ có nhiều bài toán chúng ta không cần tính toán tất cả các phương án của bài toán mà cần biết dừng lại khi đã tìm được phương án đúng.
- Các công thức được vận dụng trong ví dụ này là các công thức cơ bản, quá trình biến đổi cũng không "lắt léo". Do đó, bài toán này có thể coi là ở mức độ "thông hiểu”.
Ví dụ 2.12. 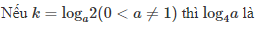
A. \[{{k}^{2}}\].
B. \[\frac{1}{{{k}^{2}}}.\]
C. \[2k.\]
D. \[\frac{1}{2k}.\]
Phân tích: Trong ví dụ này, chúng ta cần vận dụng các công thức của lôgarit để phân tích \[{{\log }_{4}}a\] theo \[{{\log }_{a}}2\]. Chú ý rằng .png) và \[{{\log }_{2}}a=\frac{1}{{{\log }_{a}}2}\]. Từ đó tìm ra phương án đúng cho bài toán.
và \[{{\log }_{2}}a=\frac{1}{{{\log }_{a}}2}\]. Từ đó tìm ra phương án đúng cho bài toán.
Hướng dẫn giải
Ta có \[{{\log }_{4}}a\] = \[{{\log }_{{{2}^{2}}}}a=\frac{1}{2}{{\log }_{2}}a=\frac{1}{2{{\log }_{a}}2}=\frac{1}{2k}.\]
Vậy D là phương án đúng.
Ví dụ 2.13. Nếu \[a={{\log }_{14}}7\] thì \[{{\log }_{4}}14\]
A. \[\frac{2}{7(1-a)}.\]
B. \[\frac{1}{2(1-a)}.\]
C. \[\frac{1}{2(1-a)}.\]
D. \[\frac{2}{1-a}.\]
Phân tích: Trong ví dụ này, chúng ta cần vận dụng các công thức của lôgarit để phân tích \[{{\log }_{4}}14\] theo \[{{\log }_{14}}7\]. Chú ý rằng .png) và 14 = 2.7. Từ đó tìm ra phương án đúng cho bài toán.
và 14 = 2.7. Từ đó tìm ra phương án đúng cho bài toán.
Hướng dẫn giải
Ta có
\[{{\log }_{4}}14={{\log }_{{{2}^{2}}}}14=\frac{1}{2}{{\log }_{2}}14=\frac{1}{2{{\log }_{14}}2}=\frac{1}{2{{\log }_{14}}(\frac{14}{7})}\]
\[=\frac{1}{2({{\log }_{14}}14-{{\log }_{14}}7)}=\frac{1}{2(1-a)}.\]
Vậy C là phương án đúng.
Nhận xét: Có thể nhận thấy rằng, bên cạnh việc vận dụng các công thức lôgarit, chúng ta cần sử dụng kĩ năng biến đổi các biểu thức hữu tỉ để tìm ra phương án cho bài toán trong ví dụ nêu trên. Do đó, bài toán trong ví dụ này có thể được xếp ở mức độ "vận dụng".
Ví dụ 2.14. (Câu 19, Đề minh hoạ môn Toán kì thi THPT Quốc gia năm 2017 của Bộ GD&ĐT)
Đặt \[a={{\log }_{2}}3,b={{\log }_{5}}3.\] Hãy biểu diễn \[{{\log }_{6}}45\] theo a và b.
A. \[{{\log }_{6}}45=\frac{a+2ab}{ab}.\]
B. \[{{\log }_{6}}45=\frac{2{{a}^{2}}-2ab}{ab}.\]
C. \[{{\log }_{6}}45=\frac{a+2ab}{ab+b}.\]
D. \[{{\log }_{6}}45=\frac{2{{a}^{2}}-2ab}{ab+b}.\]
Phân tích: Trong ví dụ này, chúng ta cần vận dụng các công thức của lôgarit để phân tích \[{{\log }_{6}}45\] theo \[{{\log }_{2}}3\] và \[{{\log }_{5}}3\]. Từ đó tìm ra phương án đúng cho bài toán.
Hướng dẫn giải
Ta có
\[{{\log }_{6}}45={{\log }_{6}}({{5.3}^{2}})={{\log }_{6}}5+{{\log }_{6}}{{3}^{2}}=\frac{1}{{{\log }_{5}}6}+2{{\log }_{6}}3=\frac{1}{{{\log }_{5}}(2.3)}+\frac{2}{{{\log }_{3}}(2.3)}\]
\[=\frac{1}{{{\log }_{5}}2+{{\log }_{5}}3}+\frac{2}{{{\log }_{3}}2+1}=\frac{1}{{{\log }_{5}}3.{{\log }_{3}}2+{{\log }_{5}}3}+\frac{2}{\frac{1}{{{\log }_{2}}3}+1}\]
\[=\frac{1}{\frac{{{\log }_{5}}3}{{{\log }_{2}}3}+{{\log }_{2}}3}+\frac{2}{\frac{1}{{{\log }_{2}}3}+1}=\frac{1}{\frac{b}{a}+b}+\frac{2}{\frac{1}{a}+1}=\frac{1}{b(\frac{1}{a}+1)}+\frac{2}{\frac{1}{a}+1}\]
\[=\frac{a}{b(a+1)}+\frac{2a}{a+1}=\frac{a+2ab}{ab+b}\]
Vậy C là phương án đúng.
Nhận xét: Có thể nhận thấy rằng, bên cạnh việc vận dụng các công thức lôgarit, chúng ta cần sử dụng kĩ năng biến đổi các biểu thức hữu tỉ để tìm ra phương án cho bài toán trong ví dụ nêu trên. Do đó, bài toán trong ví dụ này có thể được xếp ở mức độ "vận dụng".
