ĐỀ 7
Câu 1. Số điểm cực trị của hàm số $y=x^{4}-4x^{2}+1$ là:
A. 3.
B. 2.
C. 1.
D. 0.
Câu 2. Đạo hàm của hàm số $y=x\sqrt{2x-3}$ là:
A. $y'=\frac{3-x}{\sqrt{2x-3}}$
B. $y'=\frac{3x-3}{\sqrt{2x-3}}$
C. $y'=\frac{1}{\sqrt{2x-3}}$
D. $y'=\frac{x}{\sqrt{2x-3}}$
Câu 3. Phát biểu nào sau đây sai?
A. Trong cơ học, đạo hàm của vận tốc theo thời gian là gia tốc của vật.
B. Hàm số f(x) có đạo hàm tại $x_{0}$ thì nó liên tục tại $x_{0}$.
C. Nếu $f'(x_{0})=0$ thì hàm số f(x) đạt cực trị tại $x=x_{0}$.
D. Giá trị cực đại của hàm số không nhất thiết là giá trị lớn nhất trên miền xác định.
Câu 4. Cho hàm số $y=x^{3}-3x+2$ có đồ thị như hình dưới.
.png)
Điều kiện của tham số m để phương trình $x^{3}-3x=m$ có hai nghiệm dương là:
A. 0 < m < 2.
B. -2 < m < 0.
C. m > 0.
D. 2 < m < 4.
Câu 5. Điều kiện nào của tham số thực m để hàm số $y=\frac{1}{3}x^{3}-(m-1)x^{2}+3(m-2)x+\frac{1}{2}$ có hai điểm cực trị x,y, thỏa mãn $x_{1}+x_{2}=4$?
A. $\exists m.$
B. m > 3.
C. m = 1.
D. m = 3.
Câu 6. Hàm f(x) có dạng $ax^{2}+bx+c$ với a $\neq$ 0, trong đó $f(1)=\frac{5}{2},f(\frac{1}{2})=-\frac{1}{2},f'(-1)=-1$. Công thức của f(x) là:
A. $x^{2}-3x+\frac{9}{4}$.
B. $2x^{2}+3x-\frac{5}{2}$
C. $x^{2}-x+2$
D. $10x^{2}-11x+\frac{5}{2}$
Câu 7. Ba điểm cực trị của đồ thị hàm số $y=x^{4}-8x^{2}+3$ tạo thành một tam giác có diện tích bằng:
A. 30.
B. 40.
C. 52.
D. 32.
Câu 8. Cho hàm số f(x) thoả mãn f'(x) = 0, $\forall x \in \mathbb{R}$. Phát biểu nào sau đây là đúng?
A. $f(x)=e^{x}$
B. f(x) = x.
C. f(x) = C, với $C\in \mathbb{R}$
D. $f(x)=\frac{1}{x}$
Câu 9. Giá trị lớn nhất và nhỏ nhất của hàm số $y=\frac{2x-1}{x-2}$ lần lượt là:
A. 1; -1.
B. 1; $-\frac{1}{2}$.
C. 2; -1.
D. 2; 1.
Câu 10. Một khu nhà ở có 200 phòng có thể cho thuê. Người chủ tính toán tổng lợi nhuận thu được phụ thuộc vào số phòng cho thuê x theo hàm số f(x)= 3000 + 15x – 0,05x$^{2}$. Để lợi nhuận thu được là lớn nhất người chủ nên cho thuê bao nhiêu căn phòng?
A. 200.
B. 100.
C. 175.
D. 150.
Câu 11. Cho a,b là các số thực thoả mãn điều kiện $b\leq 0, a^{2}+a-b=6$. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P= ab - 2a + b + 6. Giá trị của M + m bằng:
A. $\frac{284}{27}$
B. $\frac{392}{27}$
C. 10.
D. $\frac{29}{2}$
Câu 12. Biểu thức $A=8^{log_{2}3}$ có giá trị bằng:
A. 24.
B. 27.
C. 12.
D. 3.
Câu 13.Tập nghiệm của bất phương trình $x^{\frac{2}{3}}>x^{\frac{1}{4}}$ là:
A. (0; 1).
B. (0; +$\infty$).
C. (1; +$\infty$).
D. (-$\infty$; 1).
Câu 14. Dân số của một Quận năm 2016 là 236981 người. Biết rằng trong 10 năm trở lại đây tỉ lệ tăng dân số mỗi năm của Quận là 2,6% và Quận thực hiện tốt chủ trương 100% trẻ em đúng độ tuổi đều vào lớp 1. Hỏi năm học 2017-2018, dự báo có bao nhiêu học sinh lớp 1 (6 tuổi) (làm tròn đến hàng chục)?
A. 5280 (học sinh).
B. 5150 (học sinh).
C. 5420 (học sinh).
D. 4150 (học sinh).
Câu 15. Tập xác định của hàm số $y=log_{x-\frac{1}{2}}(2-x)$ là:
A. (-$\infty$; 2).
B. $[\frac{1}{2};2]$
C. $(\frac{1}{2};2)$ \ {$\frac{3}{2}$}
D. $(\frac{1}{2};+\infty)$
Câu 16. Số nghiệm của phương trình $9^{x}-3.6^{x}-5.4^{x}=0$ là:
A. 2.
B. 1.
C. 0.
D, 3.
Câu 17. Nếu $a=log_{100}3$ và $b=log_{100}5$ thì:
A. $log_{100}1350=a-2b+1$
B. $log_{100}1350=3a-2b+\frac{1}{2}$
C. $log_{100}1350=3a+b+\frac{1}{2}$
D. $log_{100}1350=-3a+b+1$
Câu 18. Cho a > 0, b > 0, $a\neq 1;b\neq 1;n\in\mathbb{N}^{*}$, một học sinh tính biểu thức $P=\frac{1}{log_{a}b}+\frac{1}{log_{a^{2}}b}+...+\frac{1}{log_{a^{n}}b}$ theo các bước sau:
1. $P=log_{b}a+log_{b}a^{2}+...+log_{b}a^{n}$
2. $P=log_{b}a.a^{2}...a^{n}$
3. $P=log_{b}a^{1.2...n}$
4. $P=n! log_{b}a$
Học sinh trên đã giải sai ở bước nào?
A. 3.
B. 2.
C. 4.
D. 1.
Câu 19. Bất phương trình: $4^{x}-2.2^{x}-8<0$ có tập nghiệm là:
A. (-1; 4).
B. (0; 2).
C. {2}.
D. (-$\infty$; 2).
Câu 20. Tổng các nghiệm của phương trình $(\sqrt{2}-1)^{x}+(\sqrt{2}+1)^{x}-2\sqrt{2}=0$ là:
A. 3.
B. 1.
C. 0.
D. 4.
Câu 21: Hệ phương trình .png)
Điều kiện của tham số thực m để hệ có hai cặp nghiệm phân biệt là:
A. $m>\frac{4}{5}$
B. $m>\frac{4}{5}$ hoặc $m<-\frac{4}{5}$
.png)
D. $m<-\frac{4}{5}$
Câu 22: Phát biểu nào sau đây là đúng?
A. $\int xsinxdx=-xcosx-\int cosxdx$
B. $\int xsinxdx=xcosx+\int cosxdx$
C. $\int xsinxdx=xcosx-\int cosxdx$
D. $\int xsinxdx=xcosx+\int cosxdx$
Câu 23. Tìm $\int (x-sinx)dx$ được kết quả là:
A. $\frac{x^{2}}{2}+cosx+C$
B. $\frac{x^{2}}{2}-cosx+C$
C. $\frac{x^{2}}{2}+cosx$
D. $\frac{x^{2}}{2}-cosx$
Câu 24. Hàm số $F(x)=\frac{(x^{2}+3x)^{11}}{11}$ là một nguyên hàm của hàm số nào?
A. $f(x)=(x^{2}+3x)^{10}$
B. $f(x)=(2x+3)(x^{2}+3x)^{10}+C$
C. $f(x)=(2x+3)(x^{2}+3x)^{10}$
D. $f(x)=(x^{2}+3x)^{10}+C$
Câu 25. Điều kiện để áp dụng công thức $\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$ là:
A. n > -1.
B. n $\neq$ 0.
C. n > 0.
D. n $\neq$ -1.
Câu 26. Diện tích hình phẳng giới hạn bởi hai đường cong có phương trình: y = $x^{2}-4x+5, x = 1$ và x = 4 là:
A. 9.
B. 3.
C. 18.
D. $\frac{9}{2}$
Câu 27, Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi $y=x^{2}-4x+5$, x = 1 và x = 4 quanh trục hoành là:
A. $\frac{58\pi}{15}$ (đvtt).
B. $6\pi$ (dvtt).
C. $\frac{78}{5}$ (dvtt).
D. $\frac{78\pi}{5}$ (dvtt).
Câu 28. Người ta xả nước vào một thùng có thể tích 110 lít nước. Gọi V(t) là thể tích của nước xả vào thùng sau 1 giây. Giả sử v(t) = at + b và ban đầu thùng không chứa nước. Biết rằng, sau 10 giây thể tích nước trong bể là 2 lít nước, sau 20 giây thể tích nước trong bể là 6 lít nước. Sau bao lâu nước được xả đầy thùng?
A. 110 giây.
B. 90 giây.
C. 100 giây.
D. 120 giây.
Câu 29. Cho số phức $z=1-\frac{1}{2}i$. Giá trị của $\begin{vmatrix} z \end{vmatrix}$ bằng:
A. $\frac{\sqrt{5}}{2}$
B. $\frac{3}{2}$
C. $-\frac{3}{2}$
D. $\frac{3}{4}$
Câu 30. Điểm M(1;$\sqrt{3}$) là điểm biểu diễn hình học của số phức nào dưới đây?
A. $\sqrt{3}+i$
B. $\frac{1}{2}+\frac{i\sqrt{3}}{2}$
C. $1+i\sqrt{3}$
D. $1-i\sqrt{3}$
Câu 31. Cho phương trình $z^{3}+2z+a+i=0$, với $a\in\mathbb{R}$. Biết phương trình có nghiệm là z = -i, khi đó giá trị của a là:
A. 0.
B. 1.
C. -1.
D. 2.
Câu 32. Cho $z=2-\frac{2}{3}i$. Phần ảo của số phức w = (1-$\overline{z}$)z là:
A. $\frac{2}{9}i$
B. -2i
C. 2
D. $-\frac{2}{3}$
Câu 33. Rút gọn biểu thức $1+i+i^{2}+...+i^{2017}$ thu được kết quả?
A. 0.
B. 1 + i.
C. 1.
D. 2.
Câu 34. Cho số phức z thoả mãn $\begin{vmatrix} z+1 \end{vmatrix}$ = 2, tập hợp điểm biểu diễn số phức $w=\overline{z}-2i$ trên mặt phẳng phức là:
A. Đường tròn tâm I(1;2) và bán kính bằng 4.
B. Đường tròn tâm I(-1;-2) và bán kính bằng 4.
C. Đường tròn tâm I(1;2) và bán kính bằng 2.
D, Đường tròn tâm I(-1;-2) và bán kính bằng 2.
Câu 35. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và có độ dài là 2a. Thể tích của khối tứ diện S.BCD bằng:
A. $\frac{2}{3}a^{3}$
B. $\frac{1}{3}a^{3}$
C. $\frac{1}{9}a^{3}$
D. $\frac{2}{9}a^{3}$
Câu 36. Chọn phát biểu đúng:
A. Hai đường thẳng nằm trên hai mặt phẳng song song thì có một mặt phẳng chứa cả hai đường thẳng đó.
B. Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.
C. Hai đường thẳng nằm trên hai mặt phẳng song song thì chéo nhau.
D. Hai đường thẳng nằm trên hai mặt phẳng song song thì không có điểm chung.
Câu 37. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAB) là tam giác đều nằm trong mặt phẳng vuông góc với đáy. Khi đó, đường cao của hình chóp tính theo a là:
A. $\frac{a\sqrt{3}}{2}$
B. $a\sqrt{3}$
C. $\frac{a\sqrt{2}}{2}$
D. $a\sqrt{2}$
Câu 38. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, (a> 0), cạnh bên bằng 3a. Thể tích khối chóp đã cho là:
A. .png)
B. .png)
C..png)
D. .png)
Câu 39. Cho khối lăng trụ ABCD.A$_{1}$B$_{1}$C$_{1}$D$_{1}$ có đáy là hình bình hành. Tỉ số thể tích giữa khối chóp A$_{1}$.ABC và khối lăng trụ ABCD.A$_{1}$B$_{1}$C$_{1}$D$_{1}$ bằng:
A. $4\sqrt{7}a^{3}$.
B. $\frac{2\sqrt{7}}{3}a^{3}$
C. $\frac{3\sqrt{7}}{2}a^{3}$
D. $\frac{4\sqrt{7}}{3}a^{3}$
Câu 40. Cho tứ diện ABCD có AD = $a\sqrt{2}$, các cạnh còn lại đều bằng a. Diện tích của mặt cầu ngoại tiếp tứ diện là:
A. $\pi a^{2}$.
B. 2$\pi a^{2}$.
C. $\frac{\pi \sqrt{2}a^{3}}{3}$
D. $\frac{\pi a^{2}}{2}$
Câu 41. Cho hình chóp tam giác đều S.ABC có cạnh đáy a, mặt bên tạo với đáy góc 60°. Khoảng cách từ A đến (SBC) là:
A. $\frac{a}{\sqrt{2}}$
B. $\frac{3}{4}a$
C. $a\sqrt{3}$
D. $\frac{a\sqrt{3}}{2}$
Câu 42. Cho hình chóp tam giác đều S.ABC có SA = 2a, AB = a,(a > 0). Gọi H là hình chiếu vuông góc của A trên SC. Thể tích tứ diện SABH là:
A. $\frac{\sqrt{11}}{18}a^{3}$
B. $\frac{\sqrt{11}}{32}a^{3}$
C. $\frac{7\sqrt{11}}{96}a^{3}$
D. $\frac{7\sqrt{11}}{48}a^{3}$
Câu 43. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x + 2y + z - 6 = 0. Mặt phẳng (P) đi qua điểm nào sau đây?
A. (0;2;-2).
B. (–1;-2;-1).
C. (1;2;2).
D. (1;2;1).
Câu 44. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
($\Delta$): $\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-2}{3}$. Phương trình tham số của ($\Delta$) là:
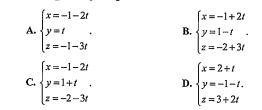
Câu 45. Trong không gian với hệ trục tọa độ Oxyz, cho phương trình mặt cầu (S): $x^{2}+y^{2}+z^{2}-2x+2z-6=0$. Tâm và đường kính của mặt cầu (s) là:
A. (1;0;-1); $R=\sqrt{10}$
B.(2;0;-2); $R=\sqrt{10}$
C. (1;0;-1); $R=2\sqrt{2}$
D. (2;0;-2); $R=\sqrt{14}$
Câu 46. Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;0;5) và đường thẳng d có phương trình: $\frac{x-1}{1}=\frac{y}{2}=\frac{z+1}{1}$. Đường thẳng đi qua A, vuông góc và cắt d có phương trình là:
.png)
Câu 47. Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng đi qua điểm M(1;0;1) và nhận $\overrightarrow{n}$(2;-2;1) làm vectơ pháp tuyến có phương trình dạng $ax+by+cz-\frac{3}{2}=0$. Giá trị của a + b + c là:
A. $-\frac{1}{2}$
B. $\frac{1}{2}$
C. $-\frac{3}{2}$
D. $\frac{3}{2}$
Câu 48. Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): $(x+3)^{2}+(y-2)^{2}+(z-1)^{2}=4$. Giao tuyến của (S) và mặt phẳng (P): x + 2y + 2z - 1 = 0 là đường tròn có bán kính bằng:
A. $\frac{2\sqrt{2}}{3}$
B. $\frac{2\sqrt{3}}{3}$
C. $\frac{8\sqrt{2}}{2}$
D. $\frac{4\sqrt{2}}{3}$
Câu 49. Trong không gian với hệ trục tọa độ Oxyz, toạ độ của điểm đối xứng với A(1;1;3) qua đường thẳng ($\Delta$): $\frac{x-1}{-1}=\frac{y-2}{2}=\frac{z+1}{-1}$ là:
A. (0; 0; -2).
B. (3; -1; -3).
C. (-3; -5; -4).
D. (-1; 2; 0).
Câu 50. Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm A(2;-1;1), B(4;2;0), C(1;-1;3) và mặt phẳng (P): 2x - y - z - $\frac{3}{2}$ = 0. Gọi M là điểm thuộc (P) sao cho $\begin{vmatrix} 2\overline{MA}+\overline{MB}+\overline{MC} \end{vmatrix}$ nhỏ nhất. Toạ độ của M là:
A. $(-1; \frac{5}{4}; \frac{-17}{4})$
B. $(0;\frac{-3}{2};\frac{1}{2})$
C. $(\frac{5}{4};\frac{-3}{4};\frac{7}{4})$
D. $(\frac{9}{4};-1;\frac{9}{2})$
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
ĐỀ 7
.png)
Hướng dẫn giải
Câu 11. Từ giả thiết suy ra $b=a^{2}+â-6\leq 0\Leftrightarrow -3\leq a\leq 2$.
Ta có P = $P=a(a^{2}+a-6)-2a+(a^{2}+a-6)+6=a^{3}+2a^{2}-7a.$
Khảo sát hàm P = $a^{3}+2a^{2}-7a$ với $-3\leq a\leq 2$ ta được .png)
.png) và $\max_{[-3;2]}P=\frac{392}{27}\Rightarrow M=\frac{392}{27}$. Do đó M + m = $\frac{284}{27}$.
và $\max_{[-3;2]}P=\frac{392}{27}\Rightarrow M=\frac{392}{27}$. Do đó M + m = $\frac{284}{27}$.
Vậy ta chọn A.
Câu 14. Gọi x (người) ($x\in N^{x}$) là số dân năm 2010 của Quận.
Khi đó số dân năm 2011 là: $x(1+\frac{2,6}{100})$.
Số dân năm 2012 là: $x(1+\frac{2,6}{100})\times (1+\frac{2,6}{100})=x(1+\frac{2,6}{100})^{2}$
Tương tự, số dân năm 2016 là $x(1+\frac{2,6}{100})^{6}$.
Vì số dân năm 2016 là 236981 nên số dân năm 2010 là $x=\frac{236981}{(1+\frac{2,6}{100})^{6}}$
Chỉ có những em sinh năm 2011 mới đủ tuổi đi học (6 tuổi) vào lớp 1 ở năm học 2017-2018. Vậy số trẻ em học lớp 1 năm học 2017-2018 là
$\frac{236981}{(1+\frac{2,6}{100})^{6}}\times \frac{2,6}{100}\approx 5280$
Vậy ta chọn A.
Câu 21. Phương trình $(1)\Leftrightarrow lnx +x=lny+y;$ ( x,y > 0)
Dùng hàm đặc trưng $\Rightarrow$ y = x.
Thay y = x vào phương trình (2), ta có $x^{2}-5mx+4=0(*)$
Hệ có 2 nghiệm thực phân biệt $\Leftrightarrow (*)$ có 2 nghiệm dương phân biệt.
Điều kiện .png)
Vậy ta chọn A.
Câu 42. Gọi K là trung điểm cạnh AB. Hai tam giác SAH và SBH bằng nhau (c.g.c) nên $\widehat{SHA}=\widehat{SHB}=90^{0}$ do đó BH $\perp$ SC. Vì vậy SC $\perp$ (ABH)
$\Rightarrow AH=SA.sin\widehat{ASC}=\frac{a\sqrt{15}}{4};SH=\sqrt{SA^{2}-AH^{2}}=\frac{7a}{4}$.
Tam giác AHB cân tại H nên HK $\perp$ AB và có
$HK=\sqrt{HA^{2}-\frac{AB^{2}}{4}}=\frac{\sqrt{11}a}{4}\Rightarrow S_{AHB}=\frac{1}{2}HK.AB=\frac{\sqrt{11}a^{2}}{8}\Rightarrow V_{S.ABH} = \frac{1}{3}S_{ABH}.SH=\frac{7\sqrt{11}a^{3}}{96}$.
Vậy ta chọn C.
Câu 50. Gọi I là điểm thỏa mãn $2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\Rightarrow I(\frac{9}{4};\frac{-5}{4};\frac{5}{4}).$
Lại có $2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=4\overrightarrow{MI}+2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=4\overrightarrow{MI}$. Vậy bài toán dẫn về việc tim M sao cho $\begin{vmatrix} \overrightarrow{MI} \end{vmatrix}$ nhỏ nhất, hay M là hình chiếu của I lên (P). Tính toán thu được $M(\frac{5}{4};\frac{-3}{4};\frac{7}{4})$. Vậy ta chọn C.
