Dạng bài tập thuộc mức độ vận dụng là bài tập yêu cầu học sinh biết sử dụng các khái niệm, các công thức để giải quyết một số vấn đề khác nhau của bài toán, chẳng hạn như sử dụng khái niệm vuông góc, tỉ lệ để xác định độ dài đường cao, sử dụng thể tích để tính khoảng cách từ điểm đến mặt phẳng.
Ví dụ 5.5. Cho hình chóp S.ABCD có đáy là hình thoi với tâm O, tam giác SBD vuông cân tại S, tam giác ABC đều và \[SO=\frac{a\sqrt{3}}{2}\]. Biết thể tích khối chóp S.ABCD bằng\[\frac{{{a}^{3}}}{8}\] , khi đó khoảng cách từ điểm C đến mặt phẳng (SBD) là
A. \[\frac{a}{2}\].
B. \[\frac{a}{4}\].
C. \[\frac{a\sqrt{3}}{2}\].
D. \[\frac{3a}{4}\].
Phân tích: Đối với bài toán tính khoảng cách từ một điểm đến một mặt phẳng, trong tình huống này, thông thường có hai phương pháp để tính
- Dựa vào công thức thể tích khối chóp S.BCD.
- Tìm hình chiếu vuông góc H của điểm C đến mặt phẳng (SBD) và tính độ đài CH.
Hướng dẫn giải
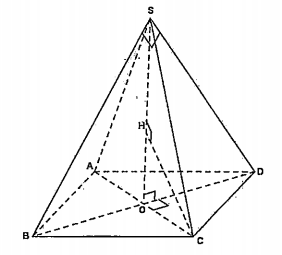
Vì tam giác SBD vuông cân tại S, suy ra
\[BO=\frac{1}{2}BD=SO=\frac{a\sqrt{3}}{2}\] và \[SB=SD=\frac{a\sqrt{6}}{2},\]
Tam giác ABC đều có đường cao \[BO=\frac{a\sqrt{3}}{2}\Rightarrow AB=BC=CA=a.\]
Ta có
\[{{V}_{S.BCD}}=\frac{1}{3}d(C,(SBD)).{{S}_{SBD}}\]
\[\Rightarrow d(C,(SBD))=\frac{3{{V}_{S.BCD}}}{{{S}_{SBD}}}=\frac{\frac{3}{2}{{V}_{S.ABCD}}}{\frac{1}{2}SB.SD}=\frac{a}{4}.\]
Vậy phương án B là đúng.
Hạ \[CH\bot SO\], ta có \[CH\bot (SBD)\]. Vậy khoảng cách từ điểm C đến mặt phẳng (SBD) bằng CH.
\[{{V}_{B.SAC}}=\frac{1}{2}{{V}_{S.ABCD}}=\frac{{{a}^{3}}}{16}.\]
Từ đó suy ra \[{{s}_{\Delta SAC}}=\frac{3{{V}_{B.SAC}}}{BO}=\frac{{{a}^{2}}\sqrt{3}}{8}.\]
Xét tam giác SOC ta có \[CH=\frac{2{{S}_{\Delta SOC}}}{SO}=\frac{{{S}_{\Delta SAC}}}{SO}=\frac{a}{4}\], chúng ta cũng đi đến đáp án B là đúng.
Nhận xét: Từ hai cách giải trên, chúng ta có thể thấy rằng, việc tính khoảng cách từ điểm C đến mặt phẳng (SBD) bằng cách dùng thể tích khối chóp S.BCD nhanh gọn hơn nhiều vì giảm được nhiều bước tính toán.
Ví dụ 5.6. Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh bằng a và các góc ở đỉnh A đều bằng 60°. Thể tích của hình hộp ABCD.A'B'C'D' là
A. \[\frac{{{a}^{3}}\sqrt{2}}{12}.\]
B. \[\frac{{{a}^{3}}\sqrt{2}}{4}.\]
C. \[\frac{{{a}^{3}}\sqrt{2}}{6}.\]
D. \[\frac{{{a}^{3}}\sqrt{2}}{2}.\]
Phân tích: Bài toán này cần phát hiện được tứ diện A'ABD là tứ diện đều. Qua đó tính được đường cao của tứ diện và cũng là đường cao của hình hộp, từ đó chúng ta tính được thể tích của hình hộp.
Hướng dẫn giải
\[\widehat{BAD}=\widehat{BAA'}=\widehat{DAA'}={{60}^{0}}\Rightarrow BD=BA'=DA'=a\Rightarrow \]A'ABD là tứ diện đều cạnh a.
Hạ \[A'H\bot (ABD)\Rightarrow \]H là trọng tâm \[\Delta ABD\].
\[A'{{H}^{2}}=AA{{'}^{2}}-A{{H}^{2}}={{a}^{2}}-{{\left( \frac{2}{3}.\frac{a\sqrt{3}}{2} \right)}^{2}}=\frac{2{{a}^{2}}}{3}\]
\[A'H=\frac{a\sqrt{6}}{3},\]
\[{{V}_{A'.ABD}}=\frac{1}{3}A'H.{{S}_{\Delta ABD}}=\frac{1}{3}.\frac{a\sqrt{6}}{3}.\frac{1}{2}.\frac{a\sqrt{3}}{2}.a=\frac{{{a}^{3}}\sqrt{2}}{12}\]
\[\Rightarrow {{V}_{ABCD.A'B'C'D'}}=A'H.{{S}_{ABCD}}=2A'H.{{S}_{\Delta ABD}}\]
\[=6{{V}_{A'ABD}}=\frac{{{a}^{3}}\sqrt{2}}{2}.\]
Vậy phương án D là đúng.
Ví dụ 5.7. Cho hình chóp S.ABC có cạnh SA = a, các cạnh bên tạo với đáy một góc bằng nhau và bằng 45°. Diện tích xung quanh của khối nón có đỉnh S và đáy là đường tròn ngoại tiếp tam giác ABC là:
A. \[\frac{\pi {{a}^{2}}\sqrt{2}}{2}\].
B. \[\pi {{a}^{2}}\sqrt{2}\].
C. \[\pi {{a}^{2}}\sqrt{2}\].
D. \[\pi {{a}^{2}}\sqrt{2}\].
Phân tích: Hình nón xác định trong bài toán trên, chúng ta sẽ biết được hình chiếu của đỉnh nón S trên đáy (ABC) là tâm của đường tròn ngoại tiếp tam giác ABC, từ đó tiến hành tính toán sẽ thu được đáp số của bài toán.
Hướng dẫn giải
Hạ \[SO\bot (ABC)\], khi đó theo giả thiết ta có \[\widehat{SAO}=\widehat{SBO}=\widehat{SCO}={{45}^{0}}.\]
Vậy các tam giác \[\Delta SOA,\Delta SOB,\Delta SOC\] là các tam giác vuông cân tại O.
\[\Rightarrow SA=SB=SC=a\]
và \[OA=OB=OC=\frac{a}{\sqrt{2}}.\]
Vậy 0 là tâm đường tròn ngoại tiếp tam giác ABC. Diện tích xung quanh của mặt nón là:
\[{{S}_{xq}}=SA.\pi .OA=\frac{\pi {{a}^{2}}\sqrt{2}}{2}.\]
Vậy A là phương án đúng.
