Dạng bài tập mức độ vận dụng cao đòi hỏi học sinh các kĩ năng phát hiện vấn đề, sử dụng nhiều tính chất hình học mới có thể giải quyết được bài toán, chẳng hạn như cần sử dụng các yếu tố về góc, thể tích; dựng thêm hình để tính khoảng cách giữa hai đường thẳng chéo nhau.
Ví dụ 5.8. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABC). Mặt phẳng qua A vuông góc với mặt phẳng (SBC) cắt SB, SC tại trung điểm M và N. Thể tích của khối chóp S.AMN là
A. \[\frac{{{a}^{3}}}{8}.\]
B. \[\frac{{{a}^{3}}}{12}.\]
C. \[\frac{{{a}^{3}}}{32}.\]
D. \[\frac{{{a}^{3}}}{64}.\]
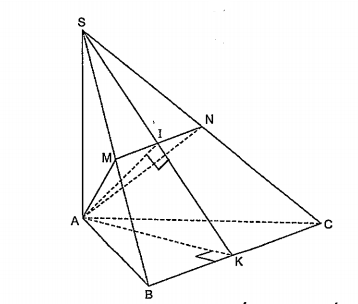
Phân tích: Bài toán này đòi hỏi học sinh phải biết vận dụng kiến thức về quan hệ vuông góc giữa hai mặt phẳng để suy ra cách tính đường cao SA của khối chóp S.ABC, từ đó sẽ tính được thể tích khối chóp S.AMN theo thể tích của khối chóp S.ABC.
Hướng dẫn giải
\[SA\bot (ABC)\Rightarrow \Delta SAB=\Delta SAC\Rightarrow AM=AN.\]
Hạ \[AI\bot MN\Rightarrow \] I là trung điểm của MN.
Kéo dài SI cắt BC tại K \[\Rightarrow \] K là trung điểm của BC và I là trung điểm của SK.
Do \[(AMN)\bot (SBC)\]
\[\Rightarrow AI\bot (SBC)\Rightarrow AI\bot SK\]
\[\Rightarrow \] Tam giác SAK vuông cân tại A \[\Rightarrow SA=AK=\frac{a\sqrt{3}}{2}.\]
Ta có: \[{{V}_{S.ABC}}=\frac{1}{3}SA.{{S}_{\Delta ABC}}=\frac{{{a}^{3}}}{8},\]
\[\frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{SM.SN}{SB.SC}=\frac{1}{4}\Rightarrow {{V}_{S.AMN}}=\frac{1}{4}{{V}_{S.ABC}}=\frac{{{a}^{3}}}{32}\]
Vậy C là đáp án đúng.
\[{{V}_{S.AMN}}=\frac{1}{3}SI.{{S}_{\Delta AMN}}=\frac{1}{6}SK.\frac{1}{2}AI.MN=\frac{{{a}^{3}}}{32}.\]
Nhận xét: Cả hai cách trên đều đòi hỏi học sinh cần phát hiện tính chất của hai mặt phẳng vuông góc để tính độ dài các cạnh và thể tích khối chóp, sau đó:
- Cách 1 dùng tỉ số thể tích giữa hai khối chóp tam giác để tính thể tích khối chóp S.AMN.
- Cách 2 dùng trực tiếp công thức thể tích để tính thể tích khối chóp S.AMN.
