1.2. NHỮNG DẠNG TOÁN THƯỜNG GẶP
Để làm tốt bài thi môn Toán, các em học sinh cần nắm vững các kiến thức và kĩ năng đã trình bày ở trên, biết vận dụng các kiến thức và kĩ năng đó giải quyết các bài tập trong sách giáo khoa và sách bài tập. Tuy nhiên, để tiếp cận với cách thi mới, phần tiếp theo chúng tôi trình bày một số dạng toán cơ bản thường gặp trong các đề thi trắc nghiệm. Trong mỗi dạng, chúng tôi cố gắng đưa ra các phân tích và cách làm theo cả phương pháp "tự luận" và phương pháp "trắc nghiệm" để làm nổi bật sự khác nhau giữa chúng cũng như ưu nhược điểm của mỗi phương pháp khi giải bài toán trắc nghiệm, qua đó các em sẽ rèn luyện được khả năng tư duy nhanh nhất để đi đến đáp số đúng của bài toán.
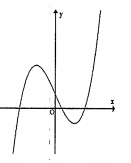
Ví dụ 1.1. (Câu 1, Đề minh hoạ môn Toán kì thi THPT Quốc gia năm 2017 của Bộ GD&ĐT)
Đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. \[y=-{{x}^{2}}+x+1\].
B. \[y=-{{x}^{3}}+3x+1\].
C. \[y=-{{x}^{4}}-{{x}^{2}}+1\].
D. \[y={{x}^{3}}-3x+1\].
Hướng dẫn giải
Dựa vào đồ thị ta thấy đây là hình dạng của đồ thị hàm bậc ba, do đó ta loại bỏ được phương án A và C.
Mặt khác, đồ thị hàm số trên có hai điểm cực trị đồng thời \[\underset{x\to -\infty }{\mathop{\lim }}\,y=-\infty \] và \[\underset{x\to +\infty }{\mathop{\lim }}\,y=+\infty \]
Do đó, ta chọn phương án đúng là D.
Ví dụ 1.2. Đồ thị hàm số \[y={{x}^{4}}+2{{x}^{2}}-3\] có dạng nào trong các đồ thị dưới đây
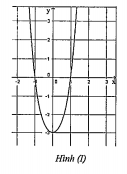
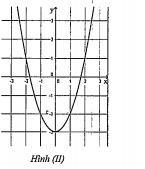
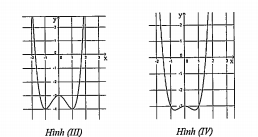
A. Hình (1). B. Hình (II). C. Hình (III). D. Hình (IV)
Hướng dẫn giải
Ta có \[y'=4{{x}^{3}}+4x,y'=0\Rightarrow x=0\], đồ thị có một cực trị, từ đó ta loại hai phương án C, D.
Xét phương án A và B, sự khác biệt là giao điểm với trục Ox.
Xét phương trình \[{{x}^{4}}+2{{x}^{2}}-3=0\Leftrightarrow \] $\left\{\begin{matrix} x=1 & \\ x=-1& \end{matrix}\right.$. Do vậy A là phương án đúng.
Nhận xét: Khi làm trắc nghiệm, một yếu tố quan trọng là chúng ta đã có bốn phương án và cố gắng tận dụng tối đa lợi thế đó so với làm tự luận. Phương pháp loại trừ là một phương pháp quan trọng cần được phát huy.
Ví dụ 1.3. Giả sử hàm số \[y=f(x)\] có bảng biến thiên như sau:
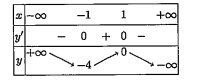
Hỏi \[y=f(x)\] là hàm số nào trong các hàm số sau?
A. \[y=-{{x}^{3}}+3x-2.\]
B. \[y=-{{x}^{4}}+x-2.\]
C. \[y=\frac{x-2}{2x-1}.\]
D. \[y={{x}^{3}}-3x+2.\]
Hướng dẫn giải
Dựa vào bảng biến thiên ta thấy đây là dạng bảng biến thiên của hàm số bậc ba. Do đó ta loại bỏ được phương án B và C.
Mặt khác, ta có đồ thị hàm số trên có hai điểm cực trị đồng thời \[\underset{x\to -\infty }{\mathop{\lim }}\,y=+\infty \] và \[\underset{x\to +\infty }{\mathop{\lim }}\,y=-\infty \].
Do đó phương án đúng là phương án A.
Ví dụ 1.4. Trong các bảng biến thiên dưới đây, bảng biến thiên nào là bảng biến thiên của hàm số \[y=\frac{x-1}{2x-1}\] ?
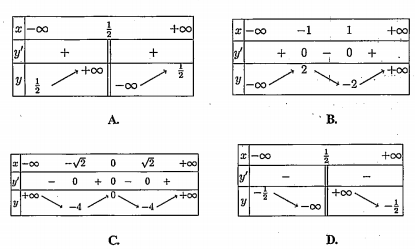
Hướng dẫn giải
Bảng biến thiên cho ở phương án B và C là dạng của hàm số bậc ba và hàm số bậc bốn. Do đó các phương án B và C là sai. Còn lại phương án A và D.
Mặt khác ta thấy \[y=\frac{x-1}{2x-1}\Rightarrow y'=\frac{1}{{{(2x-1)}^{2}}}>0\] nên hàm số đồng biến trong khoảng \[(-\infty ;\frac{1}{2})\] và \[(\frac{1}{2};+\infty )\]
Do đó phương án đúng là phương án A.
