Để tìm biểu diễn hình học của số phức z ta viết ở dưới dạng: z = a + bi với (\[a,b\in \mathbb{R}\]). Khi đó z được biểu diễn bởi điểm M(a,b) trong mặt phẳng toạ độ.
Ngược lại, điểm M có toạ độ (a;b) thì nó biểu diễn số phức z = a + bi.
Chú ý 4.10:
- Gốc toạ độ O biểu diễn số 0;
- Số phức z = a + bi là số thực khi và chỉ khi M (a;b) thuộc trục Ox;
- Số phức z = a + bi là số thuần ảo khi chỉ khi M(a;b) thuộc trục Oy;
- Số phức z = a + bi và số phức z' = a + b'i là hai số phức liên hợp với nhau khi và chỉ khi M (a;b) và M'(a';b') đối xứng với nhau qua trục Ox;
- Nếu z = a + bi và số phức z' = a + bi thì hai điểm biểu diễn của nó M(a;b) và M'(-a;b) đối xứng với nhau qua trục Oy;
– Nếu z = a + bi và số phức z' = b + ai thì hai điểm biểu diễn của nó M(a;b) và M'(b;a) đối xứng với nhau qua đường thẳng y = x.
Ví dụ 4.4. Cho số phức z = b + ai (\[a,b\in \mathbb{R}\]). Điểm M biểu diễn z trong mặt phẳng toạ độ có toạ độ là:
A.(a;b). B.(ai;b). C.(b;a). D. (b;ai).
Hướng dẫn giải
Vì hoành độ của M là phần thực của z, tung độ của M là phần ảo của nên ta chọn C.
Nhận xét: Để làm được bài toán này học sinh chỉ cần nhớ kiến thức cơ bản về biểu diễn hình học của số phức, do đó đây là một câu hỏi được xếp vào loại nhận biết.
Ví dụ 4.5. Cho \[{{z}_{1}}=2+i,{{z}_{2}}=-8+9i\] có biểu diễn hình học lần lượt là M và N. Gọi P là trung điểm của MN. Hỏi P là điểm biểu diễn của số phức nào sau đây?
A. 5 + 3i.
B. -3 + 5i.
C. 2 + 9i.
D. 55 + 4i.
Hướng dẫn giải
Dễ thấy M = (2;1), N (-8;9). Suy ra \[P(\frac{2-8}{2};\frac{1+9}{2})\] hay P(-3;5) nên ta chọn B.
Ví dụ 4.6. (Câu 31, Đề minh hoạ môn Toán kì thi THPT Quốc gia năm 2017 của Bộ GD&ĐT)
Cho số phức z thoả mãn \[(1+i)z=3-i\]. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình bên?
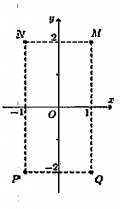
A. Điểm P.
B. Điểm Q.
C. Điểm M.
D, Điểm N.
Hướng dẫn giải
Từ \[(1+i)z=3-i\] ta suy ra \[z=\frac{3-i}{1+i}=1-2i\]. Vậy ta chọn phương án B.
Nhận xét: Để làm được bài toán này học sinh cần biết cách tìm số phức z qua việc thực hiện phép chia hai số phức, sau đó sử dụng kiến thức về biểu diễn hình học của số phức, do đó đây là một câu hỏi được xếp vào loại vận dụng.
Chú ý 4.11: Với cách làm trên ta có thể sử dụng máy tính cầm tay (chẳng hạn CASIO fx-570VN PLUS) để tìm kết quả của phép chia hai số phức sẽ nhanh hơn.
